International Harmony Based Upon A Music Of Planetary Grid Systems

by Barbara Hero

This paper will propose a method of correlating Earth Grid systems with specific musical notes, by a process of translating length to frequencies which can then be translated to musical notes. A method of octave expansion and octave reduction was used to determine the specific frequency of a note.
 
When this theory is applied to the relationships of countries to sounds, a way of increasing harmony between countries can be suggested by knowing a key note of the distance between them.

A correspondence with Pythagorean Lambdoma of seven rays is suggested. In September of 1983 I received a letter from Governors State University in Illinois requesting submission of information or research on a project called THE PLANETARY GRID SYSTEM.

I wrote back a note saying that perhaps I could help by identifying the musical interval of the modular grid system if there is a module that has been determined in length. Then, a year later in December, 1984, Bethe Hagens and William Becker sent a copy of the magazine Pursuit' which featured their research. And in this article the distances in miles of the grid-system they devised was given, so that I could get to work to determine certain musical relationships. I sent a letter detailing these relationships. After receiving my letter Bethe Hagens replied:

Thank you so much for your letter. I wanted you to know that we had received it. I am kind of stunned by what you have found in the grid — and your political interpretations. It's one of the most fascinating responses we've ever received. I don't know that I told you, but I am a professional violinist when I am not being an anthropologist. Your work in harmonics begins to get at something I have felt intuitively must exist but had no way to express.

... I have not had the time to sit with your letter and really absorb it. I will write again once I have something intelligent to say. Again, thanks so much for writing.

The Becker-Hagens report presented a theory of the growing structure of the earth, from the tetrahedron, octahedron, cube, icosahedron, and dodecahedron. These are the Platonic solids attributed to Pythagoras (500 B.C.). The dodecahedron and icosahedron together, Becker and Hagens found to be the grid system of our pre- sent age. When the line arrays of each of these solids is overlaid on a sphere, a grid emerges which they contend is a pattern the ancient peoples used for becoming one with the earth.²

Briefly, factors to consider when calculating the harmonic implications between countries, cities, or villages include the following:

• What is the great circle distance in miles between two points on the grid system?

• What are the major apex points?

• Is the assumption that Giza is the major point valid, or has the energy changed since the building of the Great Pyramid?

• Are significant places in history nodes of the grid system?

• Are fault lines energy lines?

• Are mountain ranges energy lines?

• What is the difference between the fault lines and the mountain range lines in terms of energy?

• Could certain distances portend problem areas in terms of harmonies?

The Becker-Hagens report mentioned the Twelve Devils' Graveyards Around the World (Saga Magazine, 1972)where magnetic and energy aberrations were located. These are found zigzagging the equator at 30 degrees above and 30 degrees below the equator.

Using an "Atlas" software computer program, Robert Foulkrod found the distance in miles to be 4264 miles between adjacent "Graveyards." The corresponding musical frequency based on the speed of sound in air is 0.0000502 cps. By octave expansion to the middle "C" octave (multiplying by 2 to the "n" number of times), this translates to a musical note of "A". This particular distance or musical note might be an indication of disharmony between countries, if, indeed, distance is a factor.

The Becker-Hagens report sets the kite shaped grid dimensions as 1400 miles (short end of the kite), 2200 miles (the outside kite length), and 2600 miles (the brace down the middle of the kite). The musical notes are "E flat", "A flat", and "F", respectively. The latter note represents the distance between Gomel in the Soviet Union and Sebha in Libya. Therefore the musical sound of "F" at 345 cps might be accentuated for harmony between these two countries.

The Becker-Hagens report mentioned the theory by Sinkiewitz who claimed that the present energy grid system is out of alignment with the ancient grid system, and that New Age Spiritual communities around the globe are rediscovering the new grid and building sacred sites to activate them.

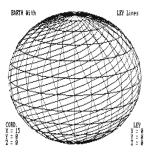
The Aleutian Islands have been predicted to be the new North Pole. See Figures 1, 2, 3, 4, & 5. What is the distance involved when a diamond of a 70 degree apex is overlaid on the new North Pole, and the legs of the diamond terminate at the Equator? This is the shape which some have found intuitively very emotionally responsive as if from a long forgotten past.

Figures 3, 4, 5

Some Visual Ways of Interpreting musical intervals, as a prelude to applying to planetary grid system.
 

The method of determining the frequency of a distance is based on formula in physics which is stated in the letter to Becker-Hagens.

v = fw
where v = (1130) the velocity of sound in air at room temperature in ft/sec,
f = frequency in cycles/sec or Hertz
w = wavelength or distance in feet.

Because of the nature of the inverse properties of wavelength and frequency, the frequency and wavelength canbe found if one knows the speed of sound for the material through which the sound travels.

Through the oceans the speed of sound would be faster and hence create a different musical note. The speed could have been taken to be the speed of sound through granite for mountainous ridges, and a different velocity in valleys, which would be of a less dense material. In valleys sound would travel slower than in the mountains, and slower still in air. One could assume that in earthquake faults the sound would travel even faster as the density of the entire earth would be a factor, it would seem, if in fact the earth is denser and not hollow.

If the earth were hollow, as has been presented by some, sound would not travel in a vacuum, and would turn to light, since light and sound are on the same spectrum separated only by our measuring sound in frequency and light in wavelength. Light would travel faster in a vacuum, slower in air, slower still in water and become sound in a dense, non-transparent medium.

The note relating two cities or sites can readily be determined by the formula described earlier. When a third city or site is added one can readily determine whether the three are in harmonic accord by using a long forgotten method of determining geometrically and algebraically the arithmetic, geometric and harmonic means.

To illustrate, take the distance from a to b to be a given length in miles, then take a distance from one of these sites to another. Put the resulting lengths end to end, bisect them and draw a circle from the halfway mark. Draw a line orthogonal to the diameter of the circle at the point on the line of the first city or site. Where this line meets the circle determines the geometric mean. Then draw a line from this point on the circle to the center of the circle. This is the arithmetic mean, and the radius of the circle. Drawing a line orthogonal to this radius stretching to the first site defines the harmonic mean. These distances can be translated into sounds which would be harmonious with each one of the cities.

For example, let us take the distance between Gomel and Timbuktu of 1400 miles, and Timbuktu to Great Zimbabwe of 2200. Lets add these in one line making a total of 3600 miles, which bisected equals 1800 miles.

The arithmetic mean would equal 1800 miles a "B" musically. The geometric mean would equal the square root of (2200 x 1400) or 1755 miles, a "C" musically and the harmonic mean 2 x (1400 x 2200) / (1400 2200), which equals 1711 miles, a "C#" musically. The length between the first two cities of 1400 is an "E flat", and the length between the second and third cities of 2200 is an "A flat". The cities exhibit an interval of a fourth between them or "A" to "E flat", which is a common harmonic used musically.

A "key note" of a country could be determined by means of a Lambdoma diagram (a Pythagorean model). See Figure 6, References 3 through 8.

The apex of the Lambdoma diagram is divided equally as the diagonal down the center of the x and y axis. The diagonal has a ratio of 1:1, so that whatever the distance is along the diagonal of the grid would be its "key note". For example Gomel in the Becker-Hagens grid has seven rays radiating from the apex point, and the diagonal which represents the "key note" extends from Gomel to El Eglab, 2600 miles, an "F" musically. From Cairo to London is 2183 miles, a "G#".

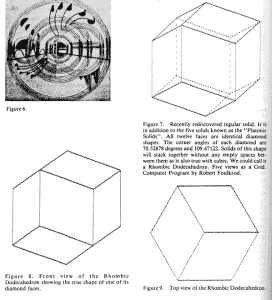
Figure 6, 7, 8, 9

Each of the rays of the grid would exhibit a unique energy, and much work has to be done to determine the quality of these differing energies. See Figures 7 & 8. In the case of the earth the circumference of the earth should be taken into account as a reference distance and frequency, the circumference is 24,860 miles. This is equivalent to a "D" musically (in air).

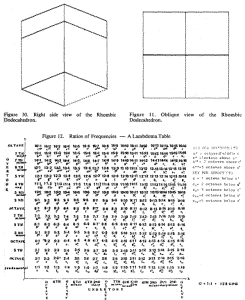
Figure 10, 11, 12

This table shows the numerical (ratio) relationships of whole numbers to specific intervals in music. When reading across the rows from left to right an undertone series results. When reading up the columns beginning at the lower left an overtone series results. Superscripts indicate the octave above middle C, and subscripts indicate the octaves below middle C.

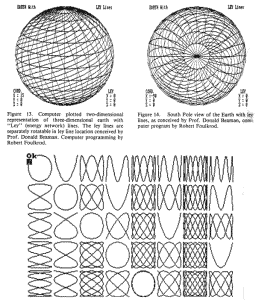
Figure 13, 14, 15

Figure 15.

Lissajous Figures. Detail of a 5x8 Lambdoma Matrix representing an earth grid evolution as defined by Pythagorean intervals in sounds. The individual patterns shown are "Lissajous" patternsformed bywhole-number ratios between a fundamental tone and its overtones and/or undertones. Computerprogram byRobert Foulkrod, programmed in "Basic" language on an IBM PC Jr.
 

Envision these Lissajous Figures arrayed on the Lambdoma Diagram matrix (Fig. 12) as a progressive series of grid lines encircling the globe of earth, each shape sounding its specific interval.

In conclusion, if the earth is in transition in terms of developing into a new phase of grid lines, this factor might indicate a shift of energy or frequency at different places on the earth. See Figure 9. The grid patterns would then take on different distances. See Figure 10. We might ask how can we as humans help the earth in this transitory phase?

First, recognizing that harmonies between cities or countries is based upon attunement to each other's energy patterns. Most of all let us attune ourselves to the earth's energies, recognizing the oneness of all things in our material universe, and learning the importance of sound as a manifestation of different realities.

Any grid system has to have distance as one of the factors, since wavelength is inherent in all sound vibrations, as the inversion of frequency. Even though we cannot hear the specific frequency of a grid line, the interval quality is present though inaudible. So lets make them audible.
 

REFERENCES

1) Becker-Hagens, "Pursuit Science: Pursuit of the Unexplained," Journal of SITU, The Society for the In-vestigation of the Unexplained, Vol. 17, Number 2, Whole Number 66, Second Quarer, 1984.

2) Jalandris, Earthfire: Exploring the Energies of the Ancients, Lincoln, Nebraska, 1981. 3) S. Levairie and E. Levy, Tone: A Study in Musical Acoustics, Kent State University Press, Kent, Ohio, 1968. 4) Kayser, Hans, Akroasis: The Theory of World Harmonics, translated by Robert Lilienfeld, Plowshare Press, Boston, 1964.

5) E. McClain, The Pythagorean Plato: Prelude to the Song Itself, Nicolas Hays, Ltd., New York,1978.

 

6) B. Hero, "Paintings Based on Relative Pitch in Music," Leonardo, Vol. 8, pp. 13-19, Pergammon Press,England, 1975.

7) B. Hero, "Drawings Based on Laser Lissajous Figures and the Lambdoma Diagram," Leonardo, Vol. 11, pp. 301-303, 1978.

8) B. Hero, "The Mathematical Laws of Sound (Relationship of Sound to Gravity)," Energy Unlimited #12, Box 288, Las Lunas, New Mexico 80731.
 

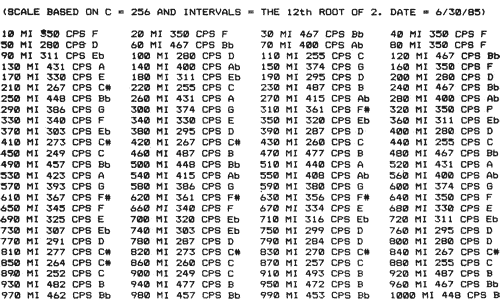
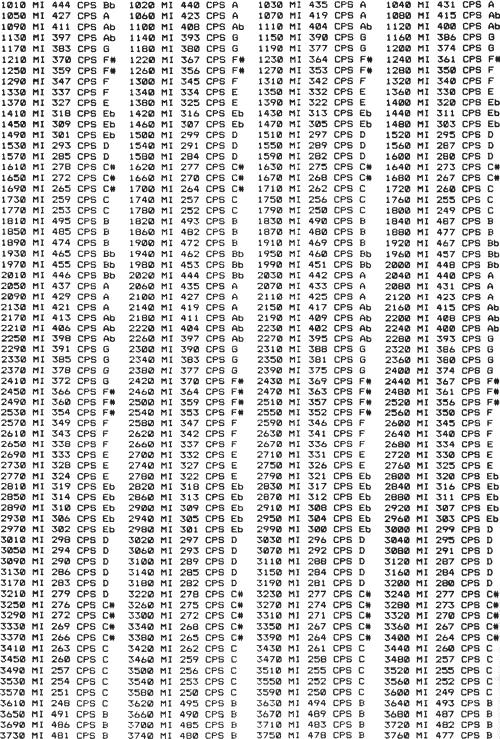
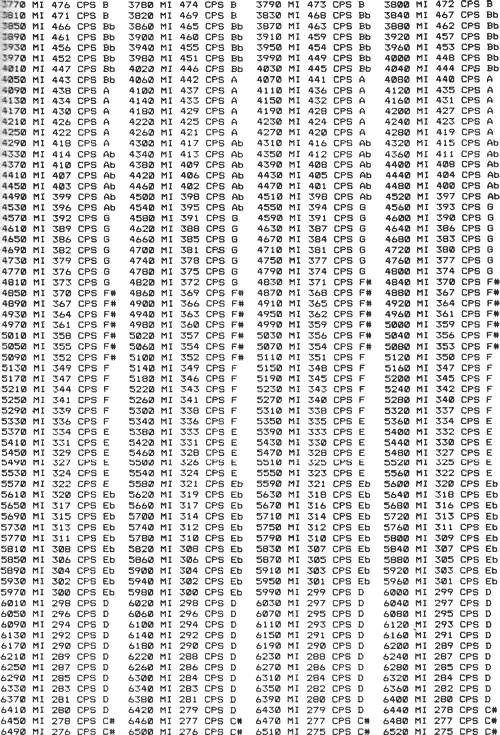
Figure 16

Table of Frequencies and Musical Notes Relative to Miles in Air

This table allows one to easily find the distance correlation in miles with musical notes and frequencies

 

Back to Contents - Antigravity And The World Grid