|

from Mid-Atlantic
Geomancy
If we want to talk with God/dess, experience has shown
that it helps to be in the right environment. Spiritual seekers from
Mayans through Christians, Native Americans, Egyptians and Hindus to
the Neolithic builders of the stone rings in Britain and Ireland
(and many more) found that by constructing their sacred places using
certain geometrical ratios - just a small handful of them - they
could more easily connect with their Maker.
Yes, it is possible to speak with our Creator anytime. However,
sacred geometry makes this easier, and different ratios make
different connections easier. The ratios have to do with different
spiritual activities like healing, foretelling
the future,
long-distance communication, levitation
and, most important, heightened ability to
communicate with our Maker. These ratios help us to
vibrate at the appropriate frequency to aid us in accomplishing the
particular spiritual activity we have in mind.
Nearly every ancient archaeological site predating recorded history,
from the Pyramids of
Egypt
and Mexico, to
Stonehenge and beyond, employs mysterious mathematical
alignments throughout their design.
These architectural formulas, rarely used today, are considered sacred
and have also been found in the way they're arranged relation to
each other and, most inexplicably, in the
Monuments of Cydonia, and the Face on Mars.
When one looks at sacred enclosures globally, there is a group of five
mathematical ratios that are found all over the world from Japan's
pagodas to Mayan temples in the Yucatan, and from Stonehenge to the
Great Pyramid. These ratios are:
-
Square Root of Two = 1.414...
-
Square Root of Three = 1.732...
-
Square Root of Five = 2.236...
-
Phi = 1.618...
Phi is the Golden Section of the Greeks.
It was said to be the first section in which the One became
many.
-
Pi = 3.1416...
Pi is found in any circle. If the diameter is 1, the
circumference is 3.1416 (C = D).
These are all irrational numbers. Pi can be taken to
1500 decimal places with no discernable pattern to it (is
that Chaos?). Let's take a closer look at each of these special
numbers, and see how we can find them in the sacred geometry
used by geomancers around the world. All five of these numbers
gain their meaning only when beaten against the One. They are all
ratios of x:1. The One is where it begins.
Pi - 3.1416 : 1 - the Circle
|
Pi (3.1416 : 1) is found in any circle. In
sacred geometry, the circle represents the spiritual
realms.
A circle, because of that transcendental number pi,
cannot be described with the same degree of accuracy as the physical
square.
The circle is yin.
It is a good shape to do all kinds of spiritual activities in. It is
good for groups to work in circles. There are many examples of
sacred spaces that are circular. |
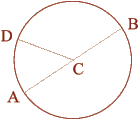
The Circle:
Radius (CD) = 1
Diameter (AB) = 2
Circumference = pi (3.1416) x Diameter |
|

Ring of Brodgar, Mainland Orkney. |
Most stone rings in the British isles are not actually circular.
Dr Alexander Thom proved this with his pioneering work in
the sixties.
Some of the true circles are Merry Maidens in
Cornwall, Stonehenge and the Ring of Brodgar.
|
Square Root of Two - 1.414 : 1 - the Square
|
In sacred geometry, the square represents the
physical world.
It can be defined totally.
If its side is one, its perimeter is exactly four, and its area
is one square - exactly.
The Square is yang. |
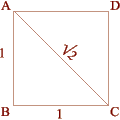
The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414 |
|

The Square Side (AB) = 1
Diagonal (AC) = Square Root of Two, 1.414 |
The square was found was in the Holy of Holies (the back room) of
Solomon's Temple (G,H,F,E).
This was where the Hebrews kept the Ark of the Covenant and
other most sacred treasures. (The dimensions here are taken from
the first part of the Ezekiel Chapter 41.) |
|
On top of
Glastonbury Tor sits an impressive stone tower.
The Tor and its tower dominate the
Somerset Levels.
This is a view taken from inside the tower looking upward.

|
 |
Square Root of Three - 1.732 : 1 - Vesica Pisces
The Vesica Pisces is created by two identical
intersecting circles, the circumference of one intersecting the
center of the other. The
vulva-shaped space thus created is called the
Vesica Pisces.
|
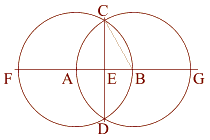 |
The Vesica Pisces:
Two Circles share a common radius (AB).
Radius AB = 1
The intersecting circles create a Vesica Pisces.
The minor axis of this Vesica Pisces (AB) = 1,
The major axis (CD) = the square root of three, 1.732
|
CB = AB |
= |
1 .....
Therefore:
|
|
a² + b² |
= |
c² |
|
.5² + x²
|
= |
1² |
|
x² |
= |
.75 |
|
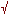 2 2
|
= |
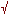 .75 .75
|
|
x |
= |
.8660 = CE
|
|
CE is 1/2 of
the major axis CD
|
|
2 CE |
= |
CD |
|
.8660 * 2
|
= |
CD |
|
CD |
= |
1.7320 =
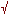 3 3
|
|
|
This is the lid of the
Chalice Well designed by Bligh Bond in the
early part of this century.
It covers one of the most
powerful Holy Wells in Britain.
The Chalice Well
has numerous examples of vesicas. |
 |
|

Gothic arch on the tower on the
Glastonbury Tor. This site was a hermitage and retreat for early
Christian monks |

Gothic arch in Gallilee of Glastonbury
Abbey. Note circular Romanesque arches behind in the Mary
Chapel. |
The top half of the
Vesica Pisces is the Gothic Arch - see
Chartres Cathedral.
It is the sacred
geometric shape of the Piscean Age. |
Square Root of Five - 2.236 : 1 - the Double Square
|
The Double Square
is found in some of the best known sacred spaces in the world, from
the King's Chamber in the Great Pyramid and Solomon's Temple in the
Bible to the interior of
Calendar II, an important underground stone chamber in
Vermont, USA.
The diagonal of a double square is to the shorter side as the square
root of five is to one.
The square root of five =
.618 + 1 + .618. |
The Double Square:
Short Side = 1
Longer Side = 2
Diagonal = Square Root of Five, 2.236 |
|
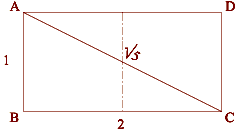
(ABCD) Double Square in Solomons Temple |
Solomons temple provides numerous examples of sacred
geometry.
The holy place (EFCD) is
the place where good Jews who had been properly cleansed could go.
This space measures twenty
cubits by forty cubits. |
Another place where a
double square is found is the
Calendar II underground chamber site in central Vermont
in the USA. It measures ten feet by twenty feet.
|

.
Calendar II, a drystone walled
underground stone chamber in central Vermont, USA. |

The interior of the chamber is 20 feet
long by 10 feet wide , or 2 to 1. The chamber is oriented
towards the Winter Solstice Sunrise. |
Phi - 1.618:1 - Ø - the Phi Rectangle
|
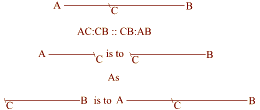
The Golden Section, Phi, 1.618:
The shorter section on the right = 3
The longer section = 5
The shorter is to the longer
as the longer is to the whole
3:5 : : 5:8 |
In the Beginning was
the One. In order to observe itself, it cut part of itself away
to make 'Other'. This Golden Section is in beautiful
proportion. As the subdividing continued away from the One,
they continued in this phi ratio.
This can be used to go
back to
the One as well. It is in this sense that three is farther away
from the One than two is.
Have you ever noticed that it is easier mathematically to go away from
One than to go towards it? In other words, it is easier to add and
multiply than it is to subtract and divide. |
3:5 : : 5:8. This ratio indicates that it is part of
this series: 1 . 2 . 3 . 5 . 8 . 13 . 21 . 34 . 55 . 89, and so on.
This is called the
Fibonacci Series. Start anywhere in the series, add the
number below, and you get the next number (for example, 21 + 13 =
34). As one ascends up the series, any number in the series, when
divided into the next one up, gets closer and closer to (but never
hits exactly) 1.618, phi, the Golden Section.
|
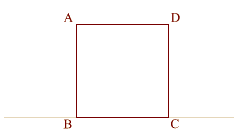
On a line create square
(ABCD) where AB = 1 |
 |
|
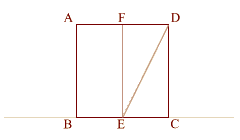
Divide lines (AD) and (BC)
in half
at (F) and (E). (BC) = 1, (EC) = .5
Double square (ECDF) is thus
created with a diameter of (ED). |
 |
|
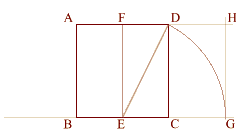
Using (ED) as a radius
swing arc from (D) downwards to 0
intersect the initial base line at (G).
Extend line (AFD), and create a
perpendicular to line (BECG) at (G)
so that it intersects line (AFD) at (H),
thus creating phi rectangle (ABGH). |
 |
|
The formula that shows
this is:
Phi = ( 1 + square root of 5 ) divided
by 2
(BE) = 1/2
(ED) = 5/2
.5 + 1.118 = 1.618 |
|
Extend arc (DG) through
(A) to (I).
Note the clear relationship between
phi and the square root of five. |
 |
|
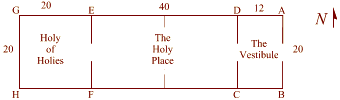 |
Solomons Temple
also contains
phi. The Vestibule (DCBA) measures twelve cubits by
twenty cubits. 12 to 20 can be reduced to 6 to 10 and further to 3
to 5.
Three and five are two
numbers in the
fibonacci series. 3/5 = 1.6, a close approximation to
1.618, or phi. |
|
Calendar I
was measured very carefully by the NEARA/ASD Earth Mysteries Group
in the early 80's.
Three measurements of the
length were taken and averaged.
The same was done with the
width. Upon dividing the length by the width, the resultant ratio
was 1.619 to 1. Phi (Ø) = 1.618 to 1. |
 |
|
 |
The Parthenon
is the Queen of Greek Temples, and personifies their interest in
Sacred Geometry. If the height of the Parthenon is 1, its
width is phi (Ø) 1.618, and its length is root
of 5= 2.236. And 1.618 + .618 = 2.236.
These are the 5 sacred geometrical ratios - Pi, (2),(3),(5) and
Phi. They are found in sacred spaces all over the world.
Remember, sacred geometry is basically simple. You must do it with
your hands, if you want to really know sacred geometry. |
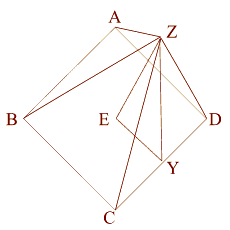
Squaring the Circle - The Great Pyramid
|
The square represents
the physical. The
circle represents the spiritual. All sacred geometers have
attempted the impossible: to square the circle (create
a square who's perimeter is equal to the circumference of a circle.)
Here is the first of two
valiant attempts:
This squaring of the circle works with a right triangle that
represents the apothem (ZY) - (a line drawn from the base of the
center of one of the sides to top of the pyramid), down to the
center of the base (ZE), and out to the point where the apothem
touches the Earth (EY). |

The Great Pyramid of Egypt
(Sphinx in foreground) |
|
 |
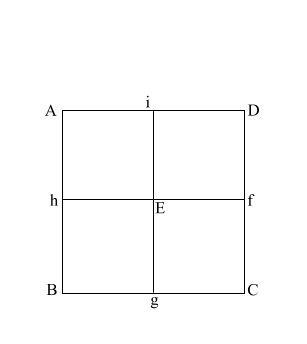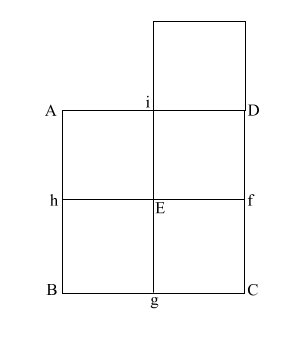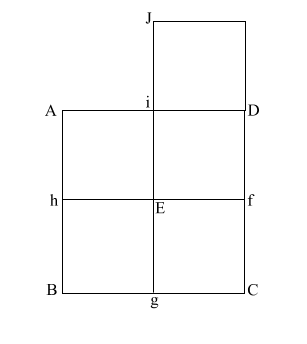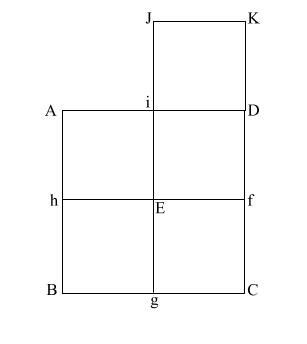
Now let's look at this in
2D,
from directly above.
For the purpose of this exercise,
the side (AB) of the base equals 2. |
|
 |
(ABCD) is the base of the
Great Pyramid.
This is lettered similarly to the wire frame version (above).
For the purpose of this exercise,
the side (AB) of the base equals 2. |
|
 |
Construct square (i JKD),
thus creating double square (JKE f). |
|
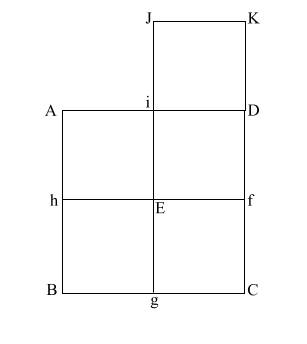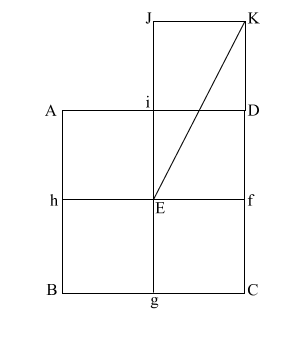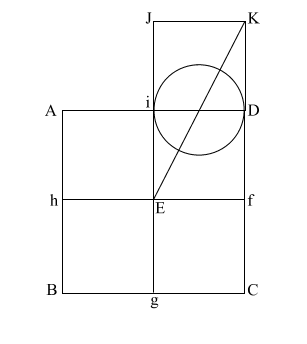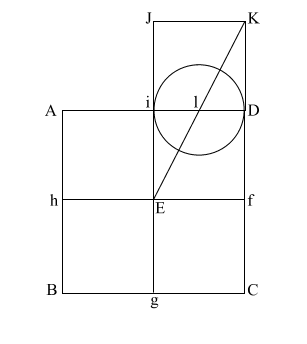 |
Create diagonal (EK)
which intersects (i D) at (l).
iD = 1,
therefore the diameter
of the circle is also 1.
(EK) = ( 5)
= .618 + 1 + .618 5)
= .618 + 1 + .618 |
|
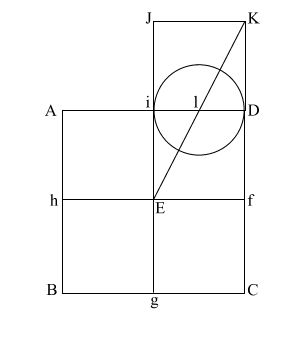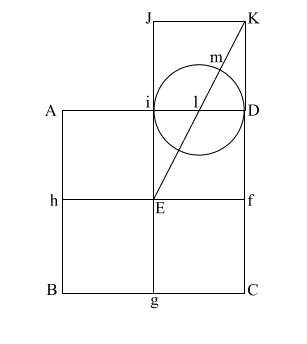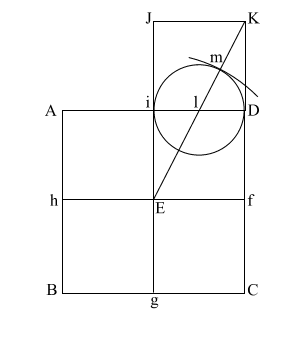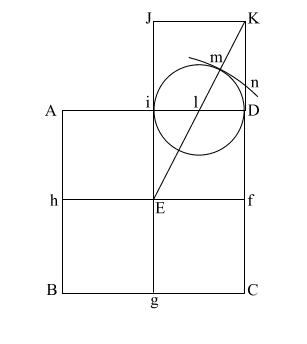 |
Put the point of your
compass at (E) and extend it along the diagonal (EK) to point (m)
where the circle intersects (EK), and draw the arc downward to
intersect (KD f C) at (n).
If (EK) = ( 5),
and (l m/l D) and l i = .5, the diameter of this circle is 1. 5),
and (l m/l D) and l i = .5, the diameter of this circle is 1.
This makes (E m) = .618 +
1, or 1.618.
(E m) is the apothem. |
|
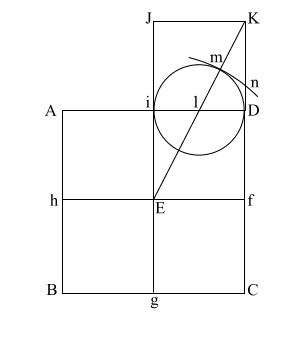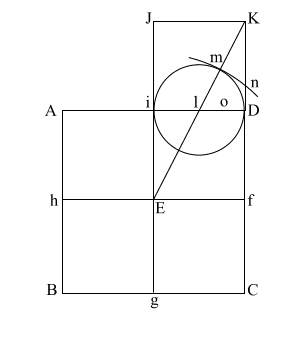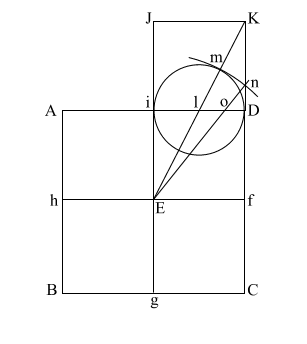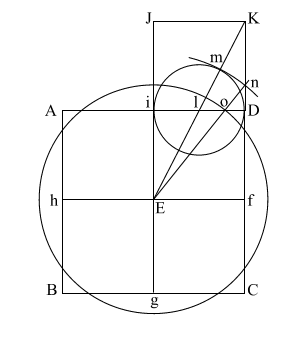 |
Draw (E n) which
intersects (A i l D ) at (o).
Put compass point at (f) and extend it to (n). Again put your point at
(E) and draw the circle which happens to have the radius (E o).
(f n) is the height of the Great Pyramid.
This circle comes remarkably close to having the same circumference as
the perimeter of the base (ABCD). |
|
Let's go back to the
original right triangle (EYZ)
(EY) = .5
(YZ) = phi
(EZ) = ( phi) phi)
EY = .5, The apothem is phi/1.618. This makes the 51 degree + degree
angle.
Using a² + b² = c², this makes the height the square root of phi.
|
Squaring the Circle - The Earth & the Moon
|
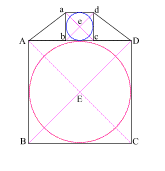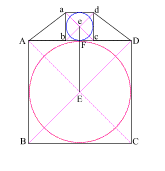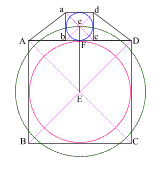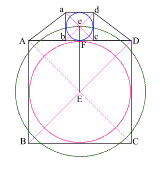
Create a square (ABCD)
with (AB) = 11
Create diagonals (AC) and (BD) crossing at center point (E)
Construct a circle which is tangent to square (ABCD) at f |
 |
|
Construct two 3 . 4 . 5
right triangles, with the 4 . 5 angles at (A) and (D).
Connect the 5 . 3 angles creating square (abcd) with side (ab) = 3
{4 + 3 + 4 = 11, or side (AD) of square (ABCD)}
Create diagonals (ac) and (bd) centering at (e)
Create a circle that is tangent to square (abcd) at four places. |
 |
|
Draw line (Ee) which
intersects side (AD) at (F)
(EF) = the radius of the larger circle and (eF) = the radius of the
smaller circle
The larger circle thus created is to the smaller circle as the
moon is to the Earth!
With your compass point at (E), create a circle with radius (Ee)
This creates a circle whose circumference is equal to the perimeter of
square (ABCD)! |
 |
The Math:
|
1
(AB) = 11
(EF) = 1/2 of (AB) = 5.5
(ab) = 3
(eF) = 1.5
Therefore 5.5 + 1.5 = 7
The circumference of a circle is equal to two times the radius (the
diameter) times pi (3.1416).
C= 14 x 3.1416
C= 43.9824 |
2
In Square (ABCD), (AB) =
11
The perimeter of a square is four times one side. 11 x 4 = 44
According to the Cambridge Encyclopedia, the equator radius of
the
Earth is 3963 miles. The equator radius of the
Moon is 1080.
The claim is that the smaller circle (in square abcd) is to the larger
circle (in square ABCD) as the Moon is to the
Earth.
|
|
3
(EF) = 5.5
(F e) = 1.5
5.5 : 1.5 :: 3963 : 1080
5.5 / 1.5 = 3.66666
3963 / 1080 = 3.6694 - (if it had been 3960, it would have been
exact!) |
Sacred Geometry
Geomancers are interested in sacred geometry because
this is the study of the way that spirit integrates into matter - by
echoing and amplifying the geometry of nature and planetary
movements, we help to align the resonance of body/mind/spirit with
the harmonic frequencies of the above and the below.
Geomancers are interested in sacred geometry because it
has been found that certain spaces, with particular ratios, enable
the participant to resonate or vibrate at the appropriate rate that
maximizes the possibility of connection to the One.
A violin isn't built out of a cigar box! It is built with the proper
wood with the proper shape and ratios, so that it resonates
correctly for the notes/frequencies it is expected to produce.
These same principles are applied to sacred spaces to maximize
the possibility that whatever is being done there on spiritual
levels will succeed.
Definitions
Two Dimensions
I've been a student of sacred geometry for over twenty-five years.
While there has been recent interest in three-dimensional sacred
geometry based on the
Platonic Solids and in sacred sites themselves, most
sacred geometrical documents I've read talk in only two dimensions -
height and width.
Obviously there is a fourth dimension and others
beyond it that are much more complex and sophisticated. But why
does the record left to us from geomancers of the past come
primarily in two dimensions?
Two is closer to the One than three is. It's less complex. I
think one of the biggest mistakes Western geomancers have made was
to take something that is very simple and make it much more complex.
The Chartres Labyrinth strikes me as being an example of this. This
stuff is simple. If you really gnow (that is, know both rationally
and intuitively) a handful of irrational ratios - pi ( ),
phi (Ø) and the square roots of two, three and
five, you've basically got it all. ),
phi (Ø) and the square roots of two, three and
five, you've basically got it all.
Three-dimensional sacred geometry just builds on this basic handful.
Numbers
One aspect of Sacred Geometry is that it works with
irrational numbers. To go to the spiritual, one must go beyond
the rational, and it appears that some of these ratios and numbers
can lead us there. By being inside a sacred space that has been
constructed using one of a handful of these sacred geometrical
ratios, the resonance that has been set up can enhance
the possibility of your making the spiritual connection you want to
make.
So, what are these irrational numbers? Let's begin with the rational.
Rational Numbers
A rational number is a number which can be expressed as the ratio of
two integers (whole numbers), such as 1/3 or 37/22. All numbers
which, when represented in decimal notation, either stop after a
finite number of digits or fall into a repeating pattern, are
rational numbers.
Irrational Numbers
An irrational number is one that cannot be represented as a ratio of
any two whole-number integers, and consequently it does not fall
into a repeating pattern of any sort when written in decimal
notation.
All of the Sacred Geometry ratios we will be working
with, the square roots of two (1.414), three (1.732) and five
(2.238), phi (1.618) and
pi (3.1416), are all irrational numbers.
Transcendental Numbers
There are certain kinds of irrational numbers that are called
transcendental numbers. Just like irrational numbers, they are
defined by what they are not (they aren't rational numbers), yet
transcendental numbers are so identified because they are not
another sort of number, known as an algebraic number.
Any number which is a solution to a polynomial equation is an
algebraic number. A polynomial equation is a sum of one or more
terms involving the same variable raised to various powers, for
example:
7 (x5) + 5 (x3) + x = 137
Any X for which any such equation is true is an algebraic
number. Because the square root of two is a solution to the
polynomial equation,
x2 = 2
it is an algebraic number.
A transcendental number requires an infinite number of terms to be
defined exactly. That's one way of thinking of God/dess.
There are special equations to derive transcendental numbers where
the terms get smaller and smaller as you go along, so you can keep
adding them together to reach any level of accuracy you need, but
the true number cannot be reached exactly. That
is the beauty of transcendental numbers!
Pi ( =
3.1416...) is such a transcendental number. It is the only one we
will be using here with Sacred Geometry. One infinite
equation which relates to the value of pi ( =
3.1416...) is such a transcendental number. It is the only one we
will be using here with Sacred Geometry. One infinite
equation which relates to the value of pi ( )
is this: )
is this:
Pi / 4 = 1 - (1/3) + (1/5) -
(1/7) + (1/9) - (1/11) + (1/13) - (1/15) + ...and so on into
infinity.
|
































