Slide #112
TITLE: World according to Eratosthenes
DATE: 194 B.C.
AUTHOR: Eratosthenes of Cyrene
DESCRIPTION: This slide shows a 19th century reconstruction of the world view of Eratosthenes of Cyrene (275-194 B.C.). More symmetrical than accurate, its partitions were the forerunners of parallels and meridians after Dicæarchus (Slide #111). Geographic information that was gathered by Alexander the Great and his successors was the primary source used by Eratosthenes, a scholar with vision large enough to put this information into a logical framework.

There can be no doubt that before the time of Eratosthenes the ideas of the learned world on the subject of geography had assumed a more regular and systematic form. And it is certain also that these had been embodied in the form of maps, which, however imperfect, were unquestionably very superior to anything that had preceded them. The first use of world maps by the Greeks had been introduced at a very early period by Anaximander (ca. 610-546 B.C. Slide #107 ), and maps of the world were not uncommon in the time of Herodotus (ca. 489-425 B.C. Slide #109 ), though based on the crude ideas of the period, and on hasty assumptions that excited the ridicule of the famous historian. Nor can it be doubted that the discoveries resulting from the conquests of Alexander the Great (ca. 356-323 B.C.) and the extension of geographical knowledge under his successors, would have gradually found their way into such maps; but we know from frequent experience, even in modern times, how slowly established errors are discarded, and how long they maintain their ground, even in the face of more accurate information. The same thing was still more the case in ancient times, and it is highly probable that if you could now recover the map of the world as it was generally received in the time of the first Ptolemies, we should find it still retaining many of the erroneous views of Herodotus and Hecatæus (Slide #109 and Slide #108).

Eratosthenes, head of the Library at Alexandria from 240 B.C. until his death, was known as beta to his contemporaries because they considered him second in all his varied academic pursuits. More critical of these accomplishments was Strabo (63 B.C.?- A.D.24, Slide #115 ) to whom we are indebted for much of our knowledge of geography in antiquity, including the work of Eratosthenes whose relevant works, neither of which survived, were On the Measurement of the Earth and Geographica, Cleomedes summarized the former, Strabo criticized the latter. Future scholars would have a higher opinion of Eratosthenes, regarding him, "as the parent of scientific geography" and at least "worthy of alpha" in that subject, particularly for his remarkable measurement of the circumference of the earth.

It appears indeed from repeated statements of Strabo that Eratosthenes made it the object of his special attention to "reform the map of the world," as it had existed down to his time, and to reconstruct it upon more scientific principles. It is this enlarged and philosophical view of the subject which constitutes his special merit, and entitles him to be justly called "the father of systematic geography". The materials at his command were still very imperfect,and the means of scientific observation were wanting to a degree which we can, at the present-day, scarcely figure to ourselves; but the methods which he pursued were of a strictly scientific character, and his judgment was so sound that he proved in many instances to be better informed and more judicious in his inferences than geographers of two centuries later.

With regard to the fundamental idea of all geography - the position and figure of the earth - Eratosthenes adopted the views that were current among the astronomers of his day, which had been received almost without exception from the times of Aristotle (ca. 384-322 B.C.) and Euclid (ca. 300 B.C.). He regarded the earth as a sphere, placed in the center of the universe, around which the celestial sphere revolved every twenty-four hours: besides which, the sun and moon had independent motions of their own. The obliquity of the sun's course to that of the celestial sphere, was of course well known; and hence the great circles of the equinoctial, and the ecliptic, or zodiacal circle, as well as the lesser circles, called the tropics, parallel with the equinoctial, were already familiar to the astronomers of Alexandria. Moreover it appears that these conceptions, originally applied to the celestial sphere, had been already transferred in theory to the terrestrial globe. Thus the idea of the globe of the earth, as it would present itself to the mind of Eratosthenes, or any of his more instructed contemporaries, did not differ materially from that of the modern geographer. For all geographical purposes, at least as the term was understood in his day, the difference between the geocentric and the heliocentric theories of the universe would be unimportant.

But Eratosthenes had the merit of making one valuable addition to the previously existing ideas upon this subject, by a more careful and successful measurement than had ever been previously attempted, of the magnitude of the earth, or circumference of the terrestrial globe. Once the idea of a spherical earth was accepted, and that it was a perfect sphere, the measurement of this body was a logical step, even to Greek scholars who were more given to philosophical speculation than to quantification and experimentation. He was not indeed the first who had attempted the solution of this problem, which would naturally engage the attention of astronomers and geometers, as soon as it was agreed that the earth was of a spherical form. Aristotle refers to the calculation of "mathematicians" who had investigated the subject (without naming them) that the earth was 400,000 stades in circumference. This distinction may belong to Eudoxus of Cnidus (ca. 370 B.C.) who also estimated its measurement at 400,000 stades. A calculation of 300,000 stades is credited to Dicæarchus (died 296 B.C.), a student of Aristotle. Aristarchus of Samos (died 230 B.C.), has been called the "Copernicus of Antiquity" because of his early espousal of a heliocentric, rather than geocentric, view of the universe (perhaps, more properly, Copernicus should be called the "Renaissance Aristarchus"). At a later period Archimedes speaks of 300,000 stades as the measurement usually received, a statement apparently founded on the calculations of Aristarchus of Samos (died 230 B.C.), one of the earlier astronomers of the Alexandrian school. But we have no information as to the data on which these first crude attempts were based, or the mode by which he authors arrived at their results.

The method pursued by Eratosthenes was theoretically sound, and was in fact identical in principle with that which has been adopted by astronomers in modern day. The method pursued by Eratosthenes is fully stated and explained by the astronomer Cleomedes, in his work on the Circular Motion of the Heavenly Bodies. Both the method and the accuracy of Eratosthenes' well-known measurement of the earth have evoked the admiration of later workers, and his calculation is regarded as one of the greatest achievements of Greek science. While still keeping to the geocentric views of the universe, Eratosthenes started from the assumption that the sun was so distant that for practical purposes one could consider its rays parallel anywhere on earth. He observed that the rays of the sun, at midday, at the time of the summer solstice, fell directly over Syene [modern-day Aswan] and that the vertical rod of the sun dial (gnomon or style) would not cast a shadow (predicated on the assumption that Syene was situated exactly under the Tropic of Cancer). At the same time of day and year, the shadow cast by a gnomon at Alexandria, to the north of Syene, was measured by Eratosthenes as 1/50 of a proper 360° circle. He assumed that: Syene (S) and Alexandria (A) lie under the same meridian circle (longitude), although there is a difference of 2°; that rays (R1 and R2) sent down from the sun are parallel; that straight lines falling on parallel lines make alternate angles equal; and that arcs subtended by equal angles are similar. He accepted a figure of approximately 5,000 stades for the distance from Syene to Alexandria, which, according to his previous reasoning, was 1/50 of the circumference of the earth. Thus 5,000 stades x 50 equals 250,000 stades, the circumference of the earth. But as a mathematical ploy, in order to achieve a number divisible by 60 or 360, so as to correlate stades with his subdivisions or degrees, he emended this to 252,000 stades [ a stade, stadion, stadia ), originally the distance covered by a plough before turning, was 600 feet of whatever standard was used]. A conversion to modern units of measure finds Eratosthenes' calculation to be somewhere between 45,007 km (27,967 miles) to 39,690 km (24,663 miles), as compared to actual equatorial circumference of 40,075 km (24,902 miles), there has always been some controversy over the equivalent modern length of a stade as used by Eratosthenes.

The only theoretical error in this mode of calculation was in the assumption - which was inevitable in the days of Eratosthenes - that the earth was exactly spherical, instead of being as it really is, a slightly oblate spheroid, and that therefore a meridian great circle was equal to that of the equator. And the error proceeding from this cause, which would not exceed 1/300th part of the whole, is wholly unimportant as compared with the practical errors arising from the defective means of observation.

In the first place, it was assumed that Syene lay directly under the tropic, it being a well-known fact that at the summer solstice the sun could be seen from the bottom of a deep well, and that at the same time the gnomon cast no perceptible shadow. But, though these facts were perfectly correct as matters of rough observation, such as could be made by general travellers, they were far from having the precise accuracy requisite as the basis of scientific calculations. Syene is in fact situated in latitude 24° 5' 30", or nearly 37 miles to the north of the Tropic. In the next place Alexandria, instead of being exactly on the same meridian with Syene, lay in fact not less than three degrees of longitude to the west of it: an error of no trifling moment when the distance between the two was assumed as the basis of calculation. But a much graver error than either of these two was that caused by the erroneous estimate of the actual distance between the two cities. What mode of measurement had been resorted to, or how Eratosthenes arrived at his conclusion upon this point, we are wholly without information: but it may well be doubted whether he had recourse to anything like actual mensuration. Indeed the difficulty which modern experience has shown to attend this apparently simple operation, where scientific accuracy is required, renders it highly improbable that it was even attempted; and the round number of 5,000 stades at once points to its being no more than a rough approximation. But even considered as such, it exceeds the truth to a degree that one could hardly have expected, in a country so well known as Egypt, and in an age so civilized as that of the Ptolemies. Alexandria is in fact situated at a distance of about 530 geographical miles (5,300 stades ) from Syene, as measured on the map along the nearest road but the direct distance between the two, or the arc of the great circle intercepts between the two points, which is what Eratosthenes intended to measure, amounts to only 453 miles or 4,530 stades. Eratosthenes, therefore, in fixing the length of this arc at 5,000 stades, was 470 beyond the truth. But this was not all. The difference in latitude between Alexandria and Syene really amounts to only 7° 5', so that the direct distance between the two cities, supposing them to have been really situated on the same meridian (as Eratosthenes assumed them to be) would not have exceeded 4,25 miles or 4,250 stades, instead of 5,000. His arc was therefore in reality 750 stades too long.

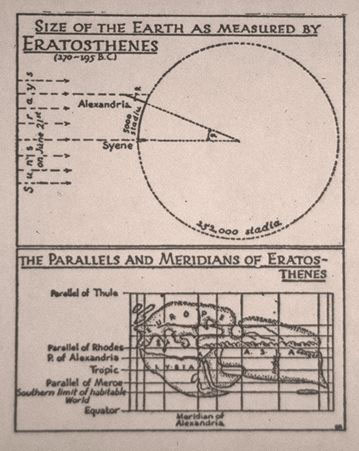
It is remarkable that while the terrestrial measurement was thus grossly inaccurate, the observation of latitude as deduced from the gnomon at Alexandria was a very fair approximation to the truth: a fiftieth part of a great circle being equivalent to an arc of 7°12', thus exceeding by about 7' only the true interval between Alexandria and Syene, while falling short of that between Alexandria and the real Tropic by about 30' or half a degree.

It appears indeed almost certain that Eratosthenes himself was aware of the imperfection of his data, and regarded the result of his calculation only as an approximation to the truth. Hence, as mentioned above, he felt himself at liberty to add 2,000 stades to the 250,000 obtained by his process, in order to have a number that would be readily divisible into sixty parts, or into degrees of 360 to a great circle.

After all it must be admitted that the calculation of Eratosthenes, considering the disadvantages under which he labored, came surprisingly near the truth. His measurement of 250,000 stades (the immediate result of his calculation) would be equivalent to 25,000 geographical miles, while the actual circumference of the earth at the equator falls very little short of 25,000 English miles. The error in excess therefore amounted to less than one-seventh part of the whole.

Once the value of 252,000 stades was accepted, it was feasible also to work out the circumference of any parallel circle. Thus Eratosthenes calculated that the parallel at Rhodes, 36°N., was under 200,000 stades in circumference. To obtain the equivalent in stades of one degree of latitude he had only to divide by 360, i.e., 700 stades; to obtain the equivalent of one degree of longitude at Rhodes he could divide, say, 195,000 stades by 360, i.e., 541.67 stades. Thus was established the basis of a fairly accurate system of coordinates for any sectional mapping of the Mediterranean based upon the Rhodes parallel.

Having thus laid the foundation of what has been called in modern times "geodesy" - the determination of the figure and dimensions of the earth, considered in its entirety, as a part of the system of the universe, Eratosthenes next proceeded to consider that portion of it which was in his time geographically known, or supposed to be inhabited. And here it must be observed that the relation between the habitable world, which was alone regarded as coming within the scope of the geographer (properly so called), and the terrestrial globe itself, was, in the days of Eratosthenes, and even long afterwards, a very different one from that which we now conceive as subsisting between them. Ever since the discoveries of the great Portuguese and Spanish navigators in the 15th and 16th centuries opened out to us new continents, and extensions of those already known, far beyond anything that had previously been suspected or imagined, men have been accustomed to regard the "map of the world" as comprising the whole surface of the globe, and including both the eastern and western hemispheres, while towards the north and south it is capable of indefinite extension, till it should reach the poles, and is in fact continually receiving fresh accessions. With the Greek geographers on the contrary, from Eratosthenes to Strabo, the known or habitable world was conceived as a definite and limited portion of the earth's surface, situated wholly within the northern hemisphere, and comprised within about a third of the extent of that section. Towards the north and south a was conceived that the excessive cold in the one case, and the intolerable heat in the other, rendered those regions uninhabitable, and even inaccessible to man. That there might be inhabitants of the southern hemisphere beyond the torrid zone, or that unknown lands might exist within the boundless and trackless ocean that was supposed to extend around two-thirds of the globe from west to east, was admitted to be theoretically possible, but was treated as mere matter of idle speculation, much as we might at the present day regard the question of the inhabitants on Mars.

In his Geographica Eratosthenes discussed the best method of drawing a map of the inhabited area of the earth as known. The first task of the geographer therefore, according to the notions then prevailing, was to determine the limits and dimensions of the map of the world which was to form the subject of his special investigations. This question, which was taken up by Eratosthenes at the beginning of his second book, had already been considered by several previous writers, who had arrived at very different results. On one point indeed they were all agreed, that the length of the habitable world, from west to east, greatly exceeded as breadth, from north to south. Democritus, two centuries before Eratosthenes, had asserted that it was half as long again as a was broad, and this view was adopted by Dicæarchus, though recent discoveries had in his day materially extended the knowledge of its eastern portions. The astronomer Eudoxus on the other hand maintained that the length was double the breadth; Eratosthenes went a step farther and determined the length to be more than double the breadth, a statement which continued to be received by subsequent geographers for more than three centuries as an established fact. According to his calculation the length of the known world from the Atlantic to the Eastern Ocean amounted to 74,000 stades, while as breadth from the parallel of the Cinnamon Country [Ethiopia/Somaliland] to that of Thule [Iceland ?] did not exceed 38,000 stades.

Therefore, as with earlier map construction, the length of the oikumene greatly exceeds the width, though by what proportion depends on how much of the northern, eastern and southern extremities was regarded as inhabited. It is clear from Strabo that Eratosthenes used an orthogonal projection. Rather than a rectangle, he thought of the oikumene as tapering off at each end of its length, like a chlamys [short Greek mantle]. Moreover Strabo tells us that to the above total of 74,000 stades Eratosthenes, using another mathematical ploy, added 2,000 at each end, to prevent the width being more than half the length. On the parallel of Rhodes, this total of 78,000 stades corresponds to about 140° longitude, which is roughly the distance from Korea to the west coat of Spain.

As approximations to sizes and shapes of parts of the world, Eratosthenes first divided the inhabited world by a line stretching from the Pillars of Hercules [Straits of Gibraltar] to the Taurus Mountains and beyond, then subdivided each of these two sections into a number of irregular shapes, or sphragides, which literally meant 'an official seal' and later was extended to represent a plot of land numbered by a government surveyor, then by extrapolation to a numbered area on a map. India he suggested drawing as a rhomboid, Ariana [the eastern part of the Persian Empire] as approximating a parallelogram. We do not know the total number of sphragides and have shapes recorded only for some. Taprobana Island, a misplaced Ceylon/Sri Lanka, and the short-cutting of Africa and India in the south were the result of the misconception that the equatorial waters were too hot to be navigated.

Eratosthenes undoubtedly conceived, in accordance with the prevalent belief in his day, that the Ocean was found immediately to the east of India, and that the Ganges flowed directly into it. Just to the north of the Ganges the great mountain chain of Imaus, which he regarded as the continuation of the Indian Caucasus and the Taurus, descended (according to his ideas) to the shores of the Eastern Ocean; and he appears to have given the name of Tarnarus to the headland which formed the termination of this great range. From that point he supposed the coast to trend away towards the north-west, so as to surround the great unknown tracts of Scythia on the north, but sending in a deep inlet to the south which formed the Caspian Sea.

Of the northern shores of Asia or Europe he had really no more knowledge than Herodotus, but, unlike that historian, he assumed the fact that both continents were bounded by the Ocean on the north; a fact which is undoubtedly true, but in a sense so widely different from that supposed by Eratosthenes that a can hardly be held as justifying his theory. In fact the conclusion of Eratosthenes was mainly based upon the erroneous belief that the Caspian communicated with the Ocean to the north in the same manner that the Persian Gulf did to the south; a view which was adopted by all geographers for a period of three centuries, on the authority of Patrocles.

It was doubtless from the same authority that Eratosthenes derived his statement as to the dimensions of the Caspian Sea, as well as that concerning the outflow into it of the rivers Oxus and Iaxartes, which he asserts "... was well known to the Greeks". Yet the erroneous idea of its communication with the Ocean to the north sufficiently shows how questionable the information possessed by the Greeks really was.

His ideas of the geographical position and configuration of India were also in great measure erroneous. As mentioned above, he conceived it to be of a rhomboidal form, which may be regarded as a rough approximation to the truth, and he even knew that the two sides which enclosed the southern extremity were longer than the other two. But as he supposed the range of Imaus that bounded the country to the north to have its direction from west to east, while the Indus flowed from north to south, he was obliged to shift around the position of his rhomb, so as to bring the other two sides approximately parallel to the two thus assumed. Hence he conceived the projecting angle of India to have a direction towards the south-east instead of the south, and even supposed it to advance farther towards the east than the mouth of the Ganges. He appears in fact to have obtained, probably from the information collected by Patrocles, a correct general idea of the great projection of India in a southerly direction towards Cape Comorin, but was unable to reconcile this with his previously conceived notions as to its western and northern boundaries, and was thus constrained altogether to distort its position in order to make it agree with what he regarded as established conclusions. It was doubtless from the same source that he had learned the name of the Coniaci, as the people inhabiting this southernmost point of India; a name which hence forward became generally received, with slight modifications, by ancient geographers.

Physical geography, in the modern sense of the term, was still quite in its infancy in the days of Eratosthenes, and it cannot be said that he did much to impart to it a scientific character. In treating the mountain chains of Asia as one continuous range, to which he applied the name of Taurus, he may be regarded as having made a first attempt, however crude, at that systematic description of mountain ranges to which we now give the name of orography. He also arrived at a sound conclusion concerning the causes of the inundation of the Nile, a subject that must naturally have engaged the attention of a geographer resident in Egypt. On the other hand he stated a strange hypothesis, that the surplus waters of the Euphrates were carried by subterranean channels to Coele, Syria, and thence again underground so as to feed the streams which broke out near Rhinocorura and Mount Casius.

Eratosthenes also adopted, and apparently developed at considerable length, an idea first suggested by the physical philosopher Strato, that the Mediterranean and the Euxine [Black] Seas had originally no outlet, and stood in consequence at a much higher level, but that they had burst the barriers that confined them, and thus given rise to the Straits of the Bosphorus, the Hellespont and that of the columns. In proof of this theory he alleged the presence of marine shells far inland in Libya, especially near the temple of Jupiter Ammon, and on the road leading to it, as well as the deposits and springs of salt that were also found in the Libyan deserts.

This map of the known world was a very striking achievement and may be considered to be the first really scientific Greek map. Although the dimensions are not known exactly, as it was presented to the Egyptian court a may be assumed to have been fairly large. It must have been drawn as closely as possible to scale, and its influence on subsequent Greek and Roman cartography was tremendous. Indeed, with Ptolemy's inaccurate alterations to the overall dimensions of the world and the oikumene, it can be said to have affected world maps right down to the Age of Discovery.

LOCATION: (this map only exists as reconstruction)

REFERENCES:
Bagrow, L., History of Cartography, p. 33.
*Bricker, C., Landmarks in Mapmaking, p. 13.
*Brown, L.A.,The Story of Maps, p. 51.
*Bunbury, E., History of Ancient Geography, pp. 618-660.
*Dilke, O.A.W., Greek and Roman Maps, pp. 33.
Harley, J.B., The History of Cartography, Volume One, pp. 154-57,162, 381.
Raisz, E., General Cartography, p. 9.
Thrower, N.J.W., Maps and Man, p. 17.

*illustrated

Index of Ancient Maps