|
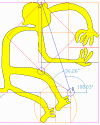
Once again, the subject of 5-pointed stars is clearly indicated by the
circumstances:
1) The Main Square's top corner (A) connects to the top right corner (B) of
the Foot-Square by a line holding 18.03 degrees with the Y-axis.
2) The Main Square's low corner (C) connects to the top right corner (B) of
the Foot-Square by a line holding 54 degrees with the Y-axis.
The angle between the two segments is practically 36 degrees, hence they facsimilate a part of the 5-pointed star. As usual, we ask if this is a
hint. Are we being told that we should complete this star here - a star,
whose one arm equals the distance A-B ?"
To appreciate the meaning of the Foot-square in the design of the
Nasca
monkey, we have to know the so called Golden Section.
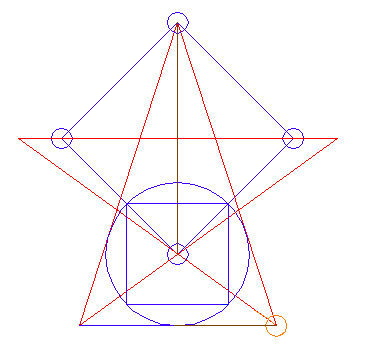
Construction of the 36-degree angle from a square
From the given 1/4 mark of a square's diagonal, draw a circle (1) through
two of the square's corners. This is the Golden Section circle. It divides
the diagonal at the point Phi so that we have three unequal length. All
three length are related by the Phi-ratio, and show the Golden Section in
its purest form.
Next, the distance from the square's center to the point Phi is taken as the
radius of the Golden circle.
If we draw the Golden circle from a corner of the square, the tangent lines
from the opposing corner to the circle form a 36 degree angle.
Construction of the regular 5-pointed star
The Golden circle's radius divides the circumcircle of the square into ten
equal parts. Thus, we can inscribe a ten-pointed star (double five-pointed
star) into the circumcircle.
But, as to the construction of any 5-pointed star from the same position,
the quickest method is based on using a single Golden circle centered in a
given corner of the square.
Step 1)
In the process, we only have to copy the original Golden circle once - to
the square's bottom corner - as opposed to having to copy it ten times onto
the square's circumcircle in the other version.
Step 2)
Underline the Golden (Phi) circle.
Step 3) Draw tangents to the Golden-circle from the opposite corner of the square,
extending to the underline of the Golden-circle. Each of these two tangents
forms one arm of the star.
Step 4)
Draw lines from the end points of the two arms of the star through the
center of the Golden Phi circle ( the low corner of the square), and
continue these as far as the horizontal diagonal of the square.
Our task is done,, because the latter two lines furnish two more arms of the
star, and the last, the fifth arm is already in place. It is the square's
horizontal diagonal extended to meet the other arms of the star.
|
 |
What purpose does this fine construction serve in this report?
The Solution to the Foot Square
The Main Square and the Foot Square from the Nasca monkey integrate into the
above diagram, as shown below.
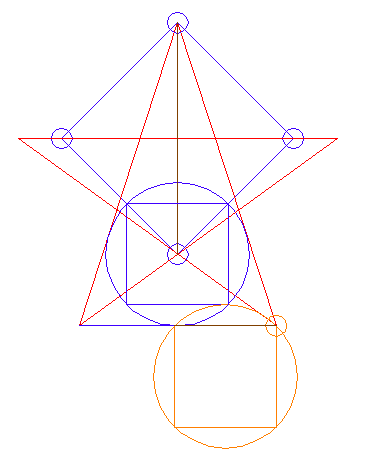
|
On the right of the diagram below, there are two superimposed circles and
two superimposed squares - the Main Square's Golden Phi-circle, and the
Foot-square's circle, and the squares inscribed in these circles.
The circles and the squares overlap with visual perfection, so that we see
only one circle and one square, as the difference between the two radii is a
mere 0.02 m, in my CAD.dwg of the monkey, which reduces to virtually nothing
on the scale shown. |
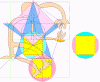 |
So, the A-B star indicated by the Foot square results from the simplest
method of constructing a 5-pointed star!!!
Our luck seems impossible, yet, we can bottle it. Anyone analyzing the
monkey figure can get the same results.
We have had here an inflow of ideas from the
Athena engraving to the
Nasca
monkey. Does the flow work in reverse, too? What if we transfer the Foot
Square design onto the Athena engraving?
|