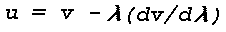
An optical mirage is a phenomenon associated with the refraction of light in the gaseous (cloud-free) atmosphere. During mirage a visible image of some distant object is made to appear displaced from the true position of the object. The image is produced when the light energy emanating from the distant source travels along a curvilinear instead of a rectilinear path, the curvilinear path, in turn, arises from abnormal spatial variations in density that are invariably associated with abnormal temperature gradients.
The visible image of the mirage can represent shape and color of the "mirrored" object either exactly or distorted. Distortions most commonly consist of an exaggerated elongation, an exaggerated broadening, or a complete or partial inversion of the object shape. Frequently, mirages involve multiple images of a single source. Under special conditions, refractive separation of the color components of white light can enhance the observation of a mirage. Atmospheric scintillation can introduce rapid variations in position, brightness, and color variations of the image.
When both the observer and the source are stationary, a mirage can be observed for several hours. However, when either one or both are in motion, a mirage image may appear for a duration of only seconds or minutes.
Although men have observed mirages since the beginning of recorded history, extensive studies of the phenomenon did not begin till the last part of the 18th century. Since that time, however, a large volume of literature has become available from which emerges a clear picture of the nature of the mirage.
The comprehensive body of information presented here is based on a survey of the literature, and constitutes the state-of-the-art knowledge on optical mirages. The report provides a ready source of up-to-date information that can be applied to problems involving optical mirages.
No claim is made that all existing pertinent writings have been collected and read. The contents of many publications, especially of those dating back to the last part of the 18th Century and the beginning of the 19th Century are evaluated from available summaries and historical reviews. Also, when a particular aspect of the mirage phenomenon is considered, the collection of pertinent literature is discontinued at the point where the state-of-the-art knowledge appears clearly defined. The collected volume of literature covers the period 1796 to 1967.
In essence, the literature survey yields the following principal characteristics of the mirage:
Only minor shortcomings appear to be evident in present knowledge of mirage phenomena. Ultimately, a unified theory is desirable that can deal with both the macroscopic and microscopic aspects. Currently, the behavior of light refraction on a large scale is represented by means of rays while the finer details are treated with the wave theory. More observations are needed that deal with the microscopic optical effects of the mirage. The finer details that arise mostly from focussing and interference are not commonly observed. They require close examination of areas that are highly selective in time and place.
The contents of this report are based on a survey of literature on atmospheric refraction in general and on optical mirages in particular. The survey began with the review of such basic sources of information on atmospheric optics as Meteorologische Optik, by Pernter and Exner, Physics of the Air, by Humphreys, The Nature of Light and Colour in the Open Air,
by Minnaert, and The Compendium of Meteorology. These sources present historical summaries, and their contents are to a large extent based on literature surveys. Key references mentioned in these sources were examined and a large volume of literature was subsequently collected by following successive reference leads. Pertinent information on atmospheric scintillation was obtained from several sources, in particular from Optical Scintillation; A Survey of the Literature, by J. R. Meyer-Arendt. A cross section of the collected literature is listed below. Because of the wide range of aspects covered, the literature is listed in the following categories:
Within each category, publications are arranged chronologically.
In category 1, descriptive accounts of mirages go back in time to 1796, when Joseph Huddart observed superior mirages near Macao. (Earlier accounts can be found in Meteorologische Optik.) Numerous recent observations of abnormal atmospheric refraction can be found in The Marine Observer. The two "classical" observations most frequently quoted as having "triggered" a long series of investigations on optical mirage are the observations of Vince and Scoresby. Vince (1798) from a position on the sea shore observed multiple images of ships, some upright and some inverted, above the ocean horizon; Scoresby (1820) observed elevated images of ships and coastal lines while navigating near Greenland. Both observations were carefully documented and results were read before bodies of the Royal Society.
Proposed theories of the mirage (category 2) are basically of three types, that are best represented by the respective works of Tait (1883), Wegener (1918), and Sir C. V. Raman (1959). Tait (in his efforts to explain the observations by Vince and Scoresby) considers a vertically
finite refracting layer having a continuous change in refractive index, and formulates the ray paths for a plane-stratified atmosphere. Wegener (motivated by mirage observations made during his stay in Greenland) replaces Tait's finite refraction layer with a "reflecting" surface - i.e. a surface of discontinuity in the refractive index - and formulates the ray paths for a spherically stratified atmosphere. Raman questions the use of geometric optics in the theory of the mirage and shows by means of physical optics that the upper boundary of the refracting layer resembles a caustic surface in the vicinity of which focussing and interference are the major mirage-producing effects. All three theories quite accurately describe various mirage observations.
Comparisons made between observation and theory (category 3) indicate that the two are compatible - i.e., abnormal light-refraction phenomena are associated with anomalous atmospheric-temperature structure. Many investigations (category 4) are concerned with determining the effects of light refraction on optical measurements made in such fields as surveying and hydrography. Corrections for refraction based on average atmospheric conditions have been computed (category 5). Of specific interest to meteorologists are the attempts to develop inversion techniques for obtaining low-level temperature structure from light-refraction measurements (category 4). The temperature profiles that can be obtained do not have the desired resolution and accuracy. During the last decade, literature on atmospheric scintillation has become extensive due to its importance to astronomy, optical communication, and optical ranging. A selected number of recent papers are presented in category 6.
The publications categorized below represent a cross section of the various endeavors that have resulted from the Earth's atmosphere having light-refraction properties. The body of information is fundamental to the contents of this report. In addition to the listed literature, many other sources of information on atmospheric optics were consulted in its production. They are referenced throughout the text, and are compiled in a bibliography at the end of the report.
| CATEGORIES |
|
1. Descriptive 2. Theoretical Models 3. Theory vs. Observation 4. Application 5. Average values 6. Atmospheric Scintillation |
| BACK TO SECTION 2 |
|
A. General B. Optical Refractive Index C. Snell's Law of Refraction D. Partial Reflections E. Spatial Variations F. Meteorological Conditions |
In a vacuum or in a medium of constant density, the energy from a light-emitting source travels along a straight line. Consequently, a distant observer sees the light source at its exact location. In a medium of variable density, such as the earth's atmosphere, the direction of energy propagation is deflected from a straight line; i.e., refracted. Refraction causes an observer to see a distant light source at an apparent position that differs from the true position by an angular distance the magnitude of which depends on the degree of refraction, i.e. on the degree of density variation between the observer and the light source. Changes in the direction of energy propagation arise principally from changes in the speed of energy propagation. The latter is directly related to density.
A clear picture of what causes refraction is obtained by means of Huygen's principle which states that each point on a wavefront may be regarded as the source or center of "secondary waves" or "secondary disturbances," At a given instant, the wavefront is the envelope of the centers of the secondary disturbances. In the case of a travelling wavefront the center of each secondary disturbance propagates in a direction perpendicular to the wavefront. When the velocity of propagation varies along the wavefront the disturbances travel different distances so that the orientation of their enveloping surface changes in time, i.e., the direction of propagation of the wavefront changes.
Practically all large-scale effects of atmospheric refraction can be explained by the use of geometrical optics, which is the method of tracing light rays -- i.e., of following directions of energy flow. The laws that form the basis of geometrical optics are the law of reflection (formulated by Fresnel) and the law of refraction (formulated by Snell). When a ray of light strikes a sharp boundary that separates two transparent media in which the velocity of light is appreciably different,
such as a glass plate or a water surface, the light ray is in general divided into a reflected and a refracted part. Such surfaces of dis- continuity in light velocity do not exist in the cloud-free atmosphere. Instead changes in the speed of energy propagation are continuous and are large only over layers that are thick compared to the optical wavelengths. It has been shown (J. Wallot, 1919) that, in this case, the reflected part of the incident radiation is negligible so that all the energy is contained in the refracted part. Since in the lower atmosphere, where mirages are most common, absorption of optical radiation in a layer of the thickness of one wavelength is negligible, Snell's law of refraction forms the basis of practically all investigations of large-scale optical phenomena that are due to atmospheric refraction (Paul S. Epstein, 1930).
The optical refractive index (n) is defined as the ratio of the velocity (v) at which monochromatic (single wavelength) light is propagated in a homogeneous, isotropic, non-conductive medium, to the velocity (c) of light in free space, i.e., n = c/v. In free space, i.e., outside the earth's atmosphere, n = 1. Thus, in the case of a monochromatic light signal travelling through a given medium, c/v > 1. In case the light signal is not monochromatic and the velocities (v) of the component waves vary with wavelength (Lambda), the energy of the signal is propagated with a group velocity u where
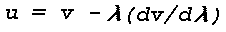
The group refractive index is given by
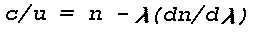
(Jenkins and White, 1957). In the visible region of the electromagnetic spectrum the dispersion, dn/d·Lambda is very small (see Table 1) and a group index is nearly equal to the index at the mean wavelength.
For a gas, the refractive index is proportional to the density rho of the gas. This can be expressed by the Gladstone-Dale relation:
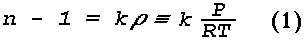
| Conditions: 5455 Å, 15°C | |
| P, mb | n |
|---|---|
| 1,000 | 1.000274 |
| 950 | 1.000260 |
| 900 | 1.000246 |
| Conditions: 5455 Å, 1013.3 mb | |
| T, °C | n |
|---|---|
| 0 | 1.000292 |
| 15 | 1.000277 |
| 30 | 1.000263 |
| Conditions: 1013.3 mb, 15°C | |
| Lambda, Å | n |
|---|---|
| 4,000 | 1.000282 |
| 5,000 | 1.000278 |
| 6,000 | 1.000276 |
| 7,000 | 1.000275 |
| 8,000 | 1.000275 |
where k is a wavelength-dependent constant, P and T are the pressure and temperature, and R is the gas constant. The refractive index of a mixture of gases, such as the earth's atmosphere, is generally assumed to obey the additive rule, that is, the total value of n-1 is equal to the sum of the contributions from the constituent gases weighted by their partial pressures. When the atmosphere is considered as a mixture of dry air and water vapor,
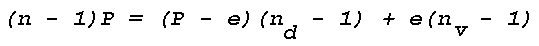
or
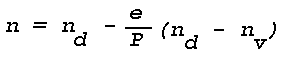
where P denotes the total pressure of the mixture, e the partial water vapor pressure and the subscripts d and v refer to dry air and water vapor, respectively. Using Eq. (1), the refractive index n of the moist air at any temperature T and pressure P can be written
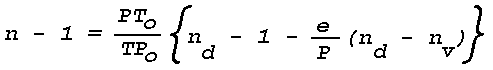
where nd and nv are the refractive indices at Po and To. For Lambda = 5455Å (about the center of the visible spectrum), at Po = 1013.3 mb (760 mm Hg) and To = 273°K, nd = 1.000292 and nv = 1.000257, so that
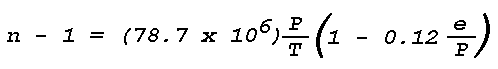
For P = 1013.3 mb, maximum values of e/P (air saturated with water vapor) for a range of tropospheric temperatures are as follows:
| T(°K) | 273 | 283 | 288 | 293 | 298 | 303 |
| e/P | 0.006 | 0.012 | 0.017 | 0.023 | 0.031 | 0.042 |
It is evident that in problems related to terrestrial light refraction the effects of humidity on the atmospheric refractive index are negligible. It is of interest to compare the formula for the optical refractive index with that for radio waves in the centimeter range. The latter can be written
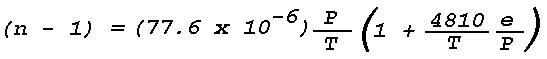
The formula for the optical refractive index can be written
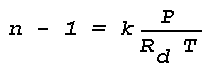
where Rd = gas constant for dry air. By introducing k as a function of wavelength (Johnson, 1954), a final expression for the optical refractive-index in the atmosphere can be written as
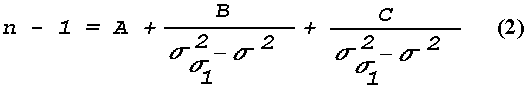
where the Sigmao2 are resonance lines and Sigma is the wavenumber in inverse microns (i.e. 1/Lambda). The latest equation is (Edlén, 1966):
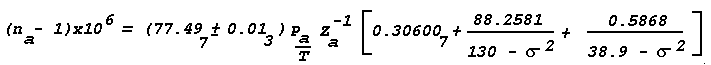
where na is the refractive index of dry air containing 0.03% CO2. Pa is the partial pressure of dry air, and Za-1 is the inverse compressibility factor for dry air (Owens, 1967). Za-1 is very close to unity; for
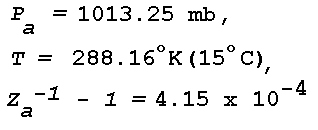
The standard value of Za-1 is assumed, i.e., the constant is
Table 1 gives the range of n for various ranges of atmospheric pressure, temperature, and wavelength. The listed values are of sufficient accuracy for a discussion of optical mirage. For a more recent version of Eq. (2) and differences in n smaller than 10-6 reference is made to the detailed work by Owens (1967).
Table 1 shows that the optical refractive index of the atmosphere is a relatively small quantity and that its largest variations with temperature, pressure and wavelength are of the order of 10-5. Such small changes in the refractive index correspond to relatively small changes in the direction of optical-energy propagation. Hence, an optical image that arises from atmospheric light refraction cannot be expected to have a large angular displacement from the light source.
Snell's law, formulated for the refraction at a boundary, may be stated as follows: the refracted ray lies in the plane of incidence, and the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant. The constant is equal to the ratio of the indices of refraction of the two media separated by the boundary. Thus, Snell's law of refraction requires that:
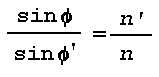
where phi and phi' are the angles of incidence and refraction respectively in the first and second medium, while n and n' are the corresponding values of the refractive index (see Fig. 1).
|
The angle of refraction (phi') is always larger than the angle of incidence (phi) when n > n', and the direction of energy propagation is from dense-to-rare. The critical angle of incidence (phic) beyond which no refracted light is possible can be found from Snell's law by substituting phi' = 90°. Thus,
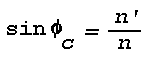
For all angles of incidence > phic the incident energy is totally reflected, and the angle of reflection equals the angle of incidence (Goos and Haenchen, 1947).
Mirages arise under atmospheric conditions that involve "total reflection." Under such conditions the direction of energy propagation is from dense-to-rare, and the angle of incidence exceeds the critical angle such that the energy is not transmitted through the refracting layer but is "mirrored." The concept of total reflection is most rigorously applied by Wegener in his theoretical model of atmospheric refraction (Wegener, 1918).
Snell's law can be put into a form that enables the construction of a light ray in a horizontal layer wherein the refractive index changes continuously. Introducing a nondimensional rectangular phi ,z coordinate system with the x-axis in the horizontal,
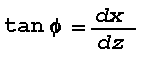
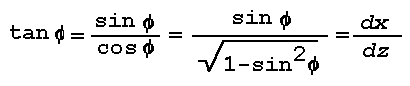
and
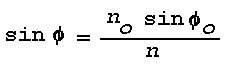
where no and phio are initial values. Substitution gives
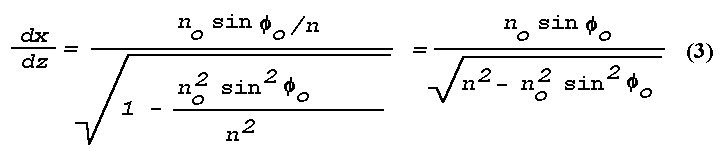
When the refractive index n is expressed as a continuous
function of x and z, the solution to the differential
equation (3) gives a curve in the x,z plane that represents
the light ray emanating to the point
(no, phio).
For example, when
Eq. (3) can be integrated in the form
For an initial refractive index no and an initial direction of
energy flow Thetaointegration between 0 and
z gives:
This equation represents a parabola. Hence, for a medium in which
n changes with z in the above prescribed fashion, the
rays emanating from a given light source are a family of parabolas.
When the ordinate of the nondimensional coordinate system is to
represent height, z must represent a quantity az',
where z' has units of height and a is the scale factor.
By introducing more complicated refractive-index profiles into Eq.
(3), the paths of the refracted rays from an extended light source
can be obtained and mirage images can be constructed. Tait and other
investigators have successfully used this method to explain various
mirage observations.
Application of Eq. (3) is restricted to light refraction in a plane-
stratified atmosphere and to refractive-index profiles that permit
its integration.
The theory of ray tracing or geometrical optics does not indicate the
existence of partial reflections, which occur wherever there is an
abrupt change in the direction of propagation of a wavefront. An
approximate solution to the wave equation may be obtained for the
reflection coefficient applicable to a thin atmospheric layer (Wait,
1962):
where R is the power reflection coefficient, Phi the angle of
incidence, Z is height through a layer bounded by
Z1 and Z2, and
Ko is the vacuum wavenumber
The equation is generally valid only when the value of R is quite
small, say
This result can be applied to atmospheric layers of known thickness
and refractive index distribution; the most convenient model is that
in which
everywhere else. Although some authors have argued that the
reflection coefficient using this model depends critically upon the
discontinuity in du/dz at the layer boundaries, it can be
shown using continuous analytic models that the results will be the
same for any functional dependence so long as the transition from
where
Delta·n is the total change in n through the
layer, and h is the thickness of the layer,
For large values of h/Lambda, and hence large values of
Alpha, the term sin (Alpha)/Alpha may be
approximated as 1/Alpha for maxima of sin Alpha. Since
h/Lambda is always large for optical wavelengths, e.g.
for a layer 1 cm thick, the power reflection coefficient may
be approximated by
Atmospheric layers with
and h = 1 cm are known to exist in the surface boundary layer,
e.g. producing inferior mirage. For visible light with a "center
wavelength" of 5.6xl0-5 cm (0.56µ),
Lambdao/h is thus 5.6x10-5. R
then becomes
This is a very small reflection coefficient, and light from even the
brightest sources reflected at normal incidence by such a layer would
be invisible to the human eye. The situation may be different at
grazing incidence or large Phi; for a grazing angle of 1°,
Phi = 89°,
and
The critical grazing angle, Thetac, for a total
reflection for the thin layer under discussion is given by
which yields a value of 0.007746 rad or 26.6'. Substituting
Since the human eye is capable of recording differences at least as
great as 3.5x10-8 (Minnaert, 1954), partial reflections of
strong light sources may occasionally be visible. The theoretical
treatment discussed here shows that as the critical angle for a
mirage is exceeded there should be a drop in reflected intensity on
the order of 10-7 - 10-8, so that instead of a
smooth transition from totally to partially reflecting regimes, there
should be a sharp decrease giving the impression of a complete
disappearance of the reflection. This is in agreement with
observation. The theory also indicates that faint images produced by
partial reflection of very bright light sources, e.g. arc lights, may
be seen at angles somewhat larger than the critical angle for a true
mirage.
As dictated by Snell's law, refraction of light in the earth's
atmosphere arises from spatial variations in the optical
refractive index. Since
according to Eq. (2), the spatial variations of n(Lambda) can
be expressed in terms of the spatial variations of atmospheric
pressure and temperature. Routine measurements of the latter two
quantities are made by a network of meteorological surface
observations and upper-air soundings. When the optical wavelength
dependence of n is neglected, Eq. (2) takes the form
and the gradient of n is given by
Optical mirages are most likely to form when atmospheric conditions
of relative calm (no heavy cloudiness, no precipitation or strong
winds) and extended horizontal visibility (<10 miles) are combined
with large radiative heating or cooling of the earth's surface. Under
these conditions the vertical gradients of pressure and temperature
are much larger than the horizontal gradients, i.e., the atmosphere
tends to be horizontally stratified.* Thus,
or
Thus, the spatial variation in the refractive index, i.e., light
refraction, depends primarily on the vertical temperature
gradient. When
ðn/ðz
is negative and the direction of energy propagation is from dense to
rare, the curvature of light rays in the earth's atmosphere is in the
same sense as that of the earth's surface. Equation (4) shows that
ðn/ðz
is negative for all vertical gradients of temperature except those
for which the temperature decreases with height
> 3.4°C/l00 m. No light refraction takes
place when
ðn/ðz
= 0; in this case
ðn/ðz
= -3.4°C/100 m. which is the autoconvective lapse
rate, i.e., the vertical temperature gradient in an atmosphere of
constant density. Table 2 gives the curvature of a light ray in
seconds of arc per kilometer for various values of
ðn/ðz
near the surface of the earth (standard P and T). When
ray curvature is positive, it is in the same sense as an earth's
curvature.
From Table 2 it is evident that two types of vertical temperature
variation contribute most to the formation of mirages; these are
temperature inversions
[(
ðT/ðZ
)>0]
and temperature lapse rates exceeding 3.4°C/100m (the
autoconvective lapse rate). Superautoconvective lapse rates cause
light rays to have negative curvature (concave upward), and are
responsible for the formation of inferior mirages (e.g., road
mirage). The curvature of the earth's surface is 33"/km, and thus
whenever there is a sufficiently strong temperature inversion, light
rays propagating at low angles will follow the curvature of the earth
beyond the normal horizon. This is the mechanism responsible for the
formation of prominent superior mirages.
The strength and frequency of vertical temperature gradients in the
earth's atmosphere are constantly monitored by meteorologists. The
largest temperature changes with height are found in the first
1,000 m above the earth's surface. In this layer, maximum
temperature gradients usually arise from the combined effects of
differential air motion and radiative heating or cooling.
The temperature increase through a low-level inversion layer can vary
from a few degrees to as much as 30°C during nighttime cooling
of the ground layer. During daytime heating, the temperature can drop
by as much as 20°C in the first couple of meters above the ground
(Handbook of Geophysics and Space Environments, 1965). Large
temperature lapses are generally restricted to narrow layers above
those ground surfaces that rapidly absorb but poorly conduct solar
radiation. Temperature inversions that are due to radiative cooling
are not as selective as to the nature of the lower boundary and are
therefore more common and more extensive than large lapses.
Temperature inversions can extend over horizontal distances of more
than 100 km. Large temperature lapses, however, do not usually extend
uninterrupted over distances more than a couple of kilometers.
At any given location, the frequency of occurrence of large
temperature lapses is directly related to the frequency of occurrence
of warm sunny days. Fig.2 shows the average distribution of
normal summer sunshine across the United States (Visher, 1954). More
than seventy percent of the possible total is recorded in a large
area extending from the Mississippi to the West Coast. Consequently,
low-level mirages associated with large temperature lapses may be
rather normal phenomena in this area. Distribution for summer and
winter of the frequency of occurrence of temperature inversions
<150 m above ground level are shown for the United States
in Fig. 3 (Hosler, 1961). The data are based on a two-year sampling
period. Figure 4 shows the distribution across the United States of
the percentage of time that the visibility exceeds 10 km (Eldridge,
1966). When Figs. 3 and 4 are combined it is seen that large areas
between roughly the Mississippi and the West Coast have a high
frequency of extended horizontal visibility and a relatively high
frequency of low-level temperature inversions. These meteorological
conditions are favorable for the formation of mirages. On the basis
of the climatic data shown in Figs. 2, 3, and 4 it can be concluded
that at some places a low-level mirage may be a rather normal
phenomenon while in other places it may be highly abnormal. An
example of the sometimes daily recurrence of superior mirage over the
northern part of the Gulf of California is discussed by Ronald Ives
(1968). Temperature inversions in the cloud-free atmosphere are often
recorded at heights up to 6,000 m above the ground. These elevated
inversions usually arise from descending air motions, although
radiative processes can be involved when very thin cirrus clouds or
haze layers are present. Narrow
layers of high-level temperature inversion, e.g., 4°C measured
in a vertical distance of a few meters, extending without
appreciable changes in height for several tens of kilometers in the
horizontal direction have been encountered (Lane, 1965). Such
inversions are conducive to mirage formation when they are
accompanied by extended visibility in the horizontal as well as in
the vertical. A climatology of such inversions can be obtained from
existing meteorological data.
Light refraction as it occurs in the earth's atmosphere can be
divided into random refraction and systematic or
regular refraction (Meyer-Arendt,1965). Random refraction is due to
the small-scale (meters or less), rapid (seconds) temperature
fluctuations associated with atmospheric turbulence, and is
responsible for such phenomena as the scintillation of stars and
planets, and the shimmer of distant objects. Systematic or regular
refraction is the systematic deviation of a propagating wavefront by
temperature gradients that are extensive in space (on the order of
several kilometers or more) and persistent in time (on the order of
an hour or more). Systematic refraction leads to the apparent
displacement of a light source from its true position. The light
source can be outside the atmosphere (astronomical refraction) or
within the atmosphere (terrestrial refraction). Random and systematic
refraction generally act simultaneously so that the associated
effects are superposed.
Values of astronomical and terrestrial refraction computed for
average atmospheric temperature structure are well documented. The
angular difference between the apparent zenith distance of a
celestial body and its true zenith distance (as observed from a
position near sea level) is zero at the zenith but gradually
increases in magnitude away from the zenith to a maximum of about 35
mm. of arc on the horizon. Thirty-five minutes of arc is very nearly
equal to the angle subtended by the sun's or moon's disc (30 mm.), so
that when these heavenly bodies appear just above the horizon they
are geometrically just below it. Figure 5 shows average values of
astronomical refraction as a function of zenith angle. The very large
increase in refraction toward the horizon causes frequently
observed distortions of the sun's or moon's disc. Normally, the
differential refraction between the point of the lower limb
(touching the horizon) and the point of the upper limb (30 min. above
the horizon) amounts to about 6 min., so that when on the horizon,
the sun or moon appears to an earth-bound observer as an ellipse
rather than a circle. Recent observations indicate that the setting
sun or moon as seen from outside the earth's atmosphere also appears
flattened due to refraction (Cameron, et al., 1963). Under
abnormal atmospheric temperature conditions, the differential
refraction can be so large that the rising or setting sun or moon
appears in grossly distorted form(O'Connell 1958).
Terrestrial-refraction angles have been computed as a function of
zenith angle and altitude of the luminous source (Link and Sekera
1940; Saunders, 1963). Depending on height, refraction angles
computed with reference to sea level vary from <5 sec. of
arc at a zenith angle of 5° to <12 min. of arc at a
zenith angle of 86°. Above 42 km refraction is negligible.
The importance of the seemingly small astronomical and terrestrial
refraction on visual observations can be evaluated as follows.
Resolving theory and practice have established that the human eye
(which is a lens system) cannot resolve, separate clearly, or
recognizably identify two points that subtend an angle to the eye of
less than 1/16° = 3.75 min. (Tolansky 1964; Minnaert,
1954). Under standard atmospheric-temperature conditions, angular
deviations due to astronomical and terrestrial refraction that are
larger than 3.75 min. occur when distant light sources are less than
about 14° above the horizon (zenith angle larger than about
76°. Hence, the effects of systematic atmospheric refraction
on visual observations of a distant light source (point source) which
is less than about 76° from the zenith can be considered
negligible because the average human eye cannot clearly separate the
source from its refracted image. However, when the luminous point
source is located at about 14° or less from the horizon, the location
and appearance of the source as seen by a distant observer are those
of its refracted image. Close to the horizon, refraction becomes
large enough to affect the visual observations of
extended sources. Thus, it is evident that the evaluation of
observations of light sources that are close to the horizon requires
knowledge of the characteristics of refracted images.
1. Geometry of Illumination and Viewing
When a luminous source is near the horizon, (i.e., near the
horizontal plane of view of its observer) the optical path length
through the atmosphere is maximum. In this case, systematic
refraction is at a maximum and the visual effects can be large when
layers of anomalous vertical temperature gradient are present. There
are, however, important practical limitations as to how much the
apparent position of a refracted image can differ from the true
position of the source. Limits in the viewing geometry can be
determined by Snell's law using limiting values of the optical
refractive index.
Observations indicate that a temperature change of 30°C across
relatively thin (<1 km) layers of temperature inversion or
temperature lapse approximates the maximum change that can be
expected (Ramdas, 1951). Thirty degrees Centigrade correspond to a
refractive-index change of about 3x10-5 (Brunt, 1929).
Combining this maximum change in the optical refractive index with
the range of values listed in Table 1, the following limits are
suggested as the range of the refractive index (n) that can be
expected in the lower cloud-free atmosphere.
Substitution of the upper and lower limit into the equation for total
reflection gives
and
Hence, when a horizontal layer or boundary across which n has
the assumed maximum variation of 1.00029 to 1.00026 is illuminated by
a light source (direction of propagation from dense to rare), the
angle of incidence has to exceed 89.5° (½° grazing
angle) in order to get total reflection and a possible mirage image.
For all practical purposes, 0.5° can be considered as the
near-maximum angle of illumination that will allow for formation of a
mirage. When the refractive index decreases with height
across the boundary and illumination is from below, the mirage image
appears at a maximum angular distance of about 1° above the true
position of the light source as illustrated in Fig. 6a . Hence,
one degree of arc must represent about the maximum angular distance
that can be expected between the true position of the light source
and its refracted image. When the image appears above the true
position of the source, the mirage is referred to as a
superior mirage. When the refractive index increases with
height and illumination is from above, an inferior mirage
appears, i.e., the image lies below the true position of the source
as shown in Fig. 6b. In terms of vertical temperature gradient, the
superior mirage is associated with an inversion and the inferior
mirage with a large temperature-lapse.
It is evident that the presence of a layer of large temperature
gradient is necessary but not sufficient for mirage formation. A
remaining requirement is the presence of light that illuminates the
layer at grazing incidence. The incident light can originate from a
physical source such as sun, moon, or planet, or it can be skylight
or sunlight reflected from the ground.
Whether the mirage is observed or not depends on the position of the
observer with respect to the light source and the refracting layer.
The planar geometry involved in a mirage observation can be
illustrated by applying Eq. (3):
to a rectangular coordinate system in which the abscissa coincides
with the ground. For simplicity it is assumed that
(i.e., the refractive index, n , decreases with height), so
that the solution to Eq. (3) represents a family of parabolas of the
form
(In applying Eq. (3), z represents az' where z'
has units of height and a is the scale factor). The family of
parabolas, sketched in Fig. 7, can be thought of as representing the
light rays from a point source located at the origin of the
coordinate system. Using the upper and lower limit
of the optical refractive index, no = 1.00029 and
n = 1.00026, the largest horizontal distance (D) is
covered by the light ray for which
Thetao = 89.5° (angles are
exaggerated in Fig. 7). All mirage images must be observed within
this distance (see Fig. 7). D can be expressed in terms of the
height (H) of the refracting layer as follows. For each member
of the family of parabolas, z is maximum at the point where
(dz/dx) = 0, i.e., at the point
Since each member is symmetric with respect to this point also,
Hence, D ~ 500H, i.e., all mirage images in this particular case
are observed within a distance from the light source that is about
500 times the thickness of the refracting layer. For example, when
the thickness of the refracting layer is 10 meters, no mirage
observations of a particular object are likely beyond a distance of
5 km. At about 5 km an image of the object may appear at an elevation
of about 0.5°, while within 5 km images may appear at
increasingly lower elevation angles until the eye can no longer
clearly separate the image from the source.
The preceding discussion applies only to the case where the observer
is located within, or at the boundary of, the mirage-producing layer,
If the observer is some distance above or below the mirage-producing
layer, mirages of much more distant objects may appear.
From the above, it is evident that principal characteristics of the
optical mirage are the small elevation angles under which the
phenomenon is observed (<1°) and the large distances
(tens of kilometers) between observer and "mirrored" object that are
possible. The geometry of the mirage explains why many observations
are made on or near horizontally extensive, flat terrain such as
deserts, lakes, and oceans and frequently involve images viewed
through binoculars (oases, ships, islands, coastal geography).
Furthermore, the above geometry illustrates that the duration of a
mirage observation is critically dependent on whether or not the
source and observer are in relative motion. For example, when the
light source is moving in such a way that the angle of illumination,
Thetao, oscillates around the critical angle, a
stationary observer located at A in Fig. 7 may see a mirage image
that alternately appears and disappears.
On the other hand, when the observer is moving relative to the source
(from A to B in Fig. 7), the mirage image can change elevation,
thereby creating an illusion of motion.
2. Number and Shape of Mirage Images
It has been recognized that systematic refraction of the light from a
single source can lead to multiple mirage images the shapes of
which can be complicated. The early observations by Vince (1798) and
Scoresby (1820) included sightings of completely or partially
inverted images of a single distant ship. From a coastal position on
the English Channel, John Parnell (1869) observed five
elevated images, all in a vertical line, of a lighthouse on the
French Coast. All five images had different shapes. During their
observations in Spain, Biot and Arago (1809) observed up to four
elevated images of a distant (161 km) light signal. The images
disappeared and reappeared intermittently and at times joined to form
a narrow vertical column of light which subsequently separated into
two parts, the lower part appearing red and the upper part appearing
green. The above observations resulted from abnormal atmospheric
light-refraction the observed images were distant, and in most cases
detailed descriptions were made with the aid of binoculars.
Practically all theoretical and experimental investigations of
optical mirages (e.g., Wollaston 1800; Hillers 1914; R. W. Wood 1911)
have been concerned with demonstrating the number and shape of
observed images. Tait's theoretical treatise and Wollaston's
laboratory experiment can be considered classical examples. Tait's
terrestrial-refraction model represents a horizontally stratified
atmosphere, and a vertically finite refracting layer with a
continuous change in refractive index. Under these assumptions the
paths of light rays are represented by the solution to the
differential equation:
where n can be expressed as a continuous function of height
(z). Tait shows that the number and shape of mirage images
depend on the detailed structure of the refractive-index profile
(temperature profile) within the refracting layer. For example, the
elevated mirage image of a distant
object becomes inverted when the refractive index in the upper part
of the refracting layer decreases more rapidly with height than in
the lower part. This "classical" explanation of image inversion is
illustrated in Fig. 8. Shown are the paths of two light rays obtained
from solving Eq. (3) for
Apparent vertical stretching (elongation, towering) of a luminous
object due to refraction is illustrated in Fig. 9. For the sake of
clarity, height and elevation angles are exaggerated. A horizontal
refracting layer is assumed that is 10 meters thick and through which
the refractive index (n) decreases with height (z) from
1.00029 to 1.00026 according to the relation
Many examples of image inversion, vertical stretching, and shrinking
due to abnormal atmospheric refraction are given in The Marine
Observer.
Tait's theoretical approach, the emphasis on the refractive-index
profile, is basic to many other theoretical investigations of the
mirage. For example, Wilhelm Hillers (1913) shows how two refracted
images of a single light source can be formed when the profile in the
refracting layer is such that the refracted rays are circular. Fig.
10 shows the
S.S. Tenagodus. Captain W. Broughton. Cape Town to Algiers.
Observers, Mr. J. J. Diston, Chief Officer, and Mr. J. F. Gristwood,
2nd Officer.
2nd March, 1955, 1730-1800 L.T. About one hour after leaving Cape
Town abnormal refraction was noticed around the horizon from SW.
through N. to E. A large tanker, 8 miles distant on the port beam,
was considerably distorted; the funnel was greatly elongated and
appeared taller then the masts, and swayed occasionally. The radar
scanner appeared suspended well above the ship. On the starboard bow,
28 miles distant, a hill 280 ft high at Ysterfontein Point was
observed to have an inverted image; these gradually telescoped until
the hill appeared as a block.
Temperatures: air 66°F, sea 59°. Slight sea, low swell.
Position of ship: 33°49'S., 18°16'E.
(Reproduced from The Marine Observer, Vol 26, No. 172, April 1956)
geometry of this special case. The refracting layer lies above the
observer and the distant light source. Refraction below the
refracting layer is assumed negligible, i.e., light rays are
rectilinear. When the light rays penetrating the refracting layer are
circles concentric about M, two separate rays emanating from the
light source reach the observer's eye and all rays intermediate and
outside these two fail to be tangent to a concentric circle.
Consequently, the observer views two separate images. An example of
three observed images of a distant hill is shown in the figure on
page 1026 in an excerpt from The Marine Observer.
Tait's approach cannot be applied indiscriminately to all mirage
phenomena because integration of Eq. (3) is restricted to a selected
range of refractive index profiles. Furthermore, the effect of the
earth's curvature is excluded so that only mirage phenomena
associated with not-too-distant objects can be considered. Hence,
Tait's model cannot explain mirage observations associated with
extraterrestrial sources such as the sun or the moon.
Alfred Wegener (1918) has developed an atmospheric refraction model
that explains distorted images of the sun, moon, planets, or stars
that are often observed near the horizon. Wegener assumes a
spherically stratified atmosphere and reduces the refracting layer to
a refracting boundary or surface of total reflection. Wegener
demonstrated that when the refracting boundary lies above the
observer and the sun is on the horizon, the boundary refracts the
solar light rays in such a way that the observer views two separate
images of the solar disc, a flattened upper image and a distorted
lower image. Fig. 11 shows the successive form of the two images for
a setting sun or moon in the presence of a 7°
temperature-inversion layer 50 m above the observer* as computed by
Wegener. The degree of deflection of the incoming light rays and
consequently the degree of distortion of the solar disc depends on
the refractive-index change or temperature change across the
reflecting boundary. When the temperature change is small, only a
single distorted image of the solar disc appears. When the change
across the boundary is
very large only the the flat upper part of the "split" solar image is
seen, so that the setting sun appears to vanish above the horizon.
When the atmosphere is highly stratified, i.e., when several
horizontal refracting boundaries are present, the setting sun can
appear like a Chinese Pagoda or like a stack of discs. The refracted
images of the setting sun computed by Wegener's model agree closely
with those photographed and described by D. J. K. O'Connell (1958)
in connection with a study of the green and red flash phenomena.
Wegener's model is not restricted to luminous sources outside the
earth's atmosphere. It can be applied to distant terrestrial objects
such as mountains from which emitted light rays are at grazing
incidence to the top of the refracting boundary. Wegener's model of
atmospheric refraction illustrates the characteristics that are basic
to many spectacular risings or settings of sun, moon, or planet.
Following are three accounts of such abnormal atmospheric-refraction
phenomena as given in The Marine Observer.
The atmospheric-refraction models of Tait and Wegener quantitatively
explain the basic characteristics of the most commonly observed
mirage-images. Other theoretical investigations are available that
discuss various special aspects. For example, the theory of the
superior mirage by Odd Haug explains the appearance of up to four
images from a single source. Wilhelm Hillers treats the special case
of a lateral mirage, i.e., the refraction of light when the
refractive-index gradient is horizontal, as may be the case along a
wall heated by solar radiation. Koji Ilidaka and Gustav Forster
discuss the theory of refraction when the surfaces of constant
density in the atmosphere are somewhere between horizontal and
vertical. Together, these theoretical models explain adequately the
varying ways in which a mirage image can appear to an observer.
Currently, there is no single model with a numerical solution
to all aspects of the mirage.
M/V. Australind. Captain J. F. Wood. Port Said to Bremen.
Observer, Mr. D. Ewan, Chief Officer.
27th April, 1950, 1546-1549 G.M.T. The accompanying sketches picture
the sequence of shapes assumed by the sun as a result of refraction.
After Clearing the horizon the sun slowly regained its normal
proportions and at an altitude of 1½° no refraction was
apparent. No land was visible near the phenomenon. Wind N, force 4.
Barometer 1020.3 mb, air temp. 58°F. Sky cloudless.
Position of ship: Latitude 38° 04'N., Longitude 9° 24'W.
(Reproduced from The Marine Observer, Vol. 21, No. 152, p. 80,
April 1951)
O.W.S. Weather Recorder. Captain A. W. Ford, At Ocean Weather
Station A. Observer, Mr. J. Ballantyne, 3rd Officer.
5th May, 1955, 2220-2240 G.M.T. Towards sunset abnormal refraction
was observed, and for a while two suns were visible. A false sun was
seen for half its
diameter on the horizon, and touching the real sun above. The real
sun was partly obscured by cloud. The false sun persisted for 3 or 4
min after the real sun had set. A vertical ray with reddish
coloration extended to about 4° above the real sun.
(Reproduced from The Marine Observer, Vol. 26, No. 172, April
1956)
M.V. Timaru Star. Captain H. W. McNeil. London to Curacao.
Observer, Mr. N. Johnson, 3rd Officer.
4th January, 1956. While proceeding down the English Channel at 0800
G.M.T., shortly after sunrise, the sun was observed to have a
distorted appearance (sketch 1). By 0810 while the sun continued to
rise a false "sun" began to set. Two minutes later there was a
distinct gap between the true sun and the false and by 0814 the false
sun was no longer visible. In the area of the rising true sun the sky
was clear and a bright orange in color. A phenomenon similar to
sketch 2 was observed at sunset on the same day.
Position of ship: 50° 05'N., 02° 04'W.
(Reproduced from The Marine Observer, Vol. 27, No. 175, p. 13,
1957)
3. Effects from Focussing and Interference
A recent theoretical and experimental investigation of the optical
mirage is presented by Sir C. V. Raman (1959). Sir C. V. Raman
demonstrates that multiple, inverted images of a single object can
arise from interference and focussing of the incident and reflected
wavefronts near the boundary of total reflection. Raman's work, which
is entirely based on wave theory, suggests the interaction of
wavefronts within a refracting layer as a mechanism in mirage
formation.
The occurrence of focussing and interference in situations that give
rise to mirage, examined specifically by Raman, is also evident from
various investigations based on geometrical optics. For example,
the crossing of light rays mentioned in connection with image
inversion implies interference of wavefronts at the points of
intersection.
The visual effects from focussing and interference must be considered
in particular when plane-parallel radiation (radiation from a very
distant source) is incident on a layer of total reflection. In this
case, there is a constant crossing of light rays within a relatively
narrow region of the refracting layer, as illustrated in Fig. 12 (for
the sake of clarity, height and elevation angles are exaggerated). In
Fig. 12, a circular collimated light-beam of diameter A is incident
on the lower boundary of a temperature-inversion layer at angle equal
to or exceeding the critical angle for total reflection. Interference
of the incident and reflected wavefronts occurs in a selected layer
near the level of total reflection. This layer, shaded in Fig. 12,
has a maximum thickness B, which is dependent on A. In
the absence of absorption, the amount of radiant energy, flowing per
unit time through Pi·A2 equals that flowing
through Pi·B2. When B is less than
A, the energy density at B is larger than at A,
so that the brightness of the refracted light beam increases in the
layer of interference.
An example of the ratio of A to B can be Given with the
aid of Eq. (3). It is assumed that the optical refractive index
through the inversion layer varies from
the level of total reflection coincides with the upper boundary of
the inversion layer. Under these conditions, it can be shown that
B/A = A/16H
where H is the thickness of the temperature-inversion layer.
When the diameter A of the incident light beam is less than
16H, B is less than A and a brightening or
focussing occurs near the top of the inversion. When the angle of
incidence of the light beam is larger than the critical angle,
~89.5°, the level of total reflection lies below the upper
boundary of the inversion layer. In this case, brightening can still
occur near the level of total reflection, but the restrictions on the
required beam-diameter become rather severe. The above example, based
on a special case, demonstrates that sudden brightening can be
encountered near the upper boundary of a refracting layer when
optical mirages are associated with a refracting layer that is thick
with respect to the diameter of the incident light beam from a
distant source and when the angle of incidence is near the critical
angle.
Observations of the brightening phenomenon must be considered rare in
view of the selective location of its occurrence within the
temperature-inversion layer and the requirement of plane-parallel
incident radiation. Upper-level inversions seem most likely to
produce the phenomenon. Some photographs showing apparent brightening
of "spike" reflections on the edge of the setting sun are shown in
O'Connell (1958, c.f., p. 158).
Microscopic effects due to interference of wavefronts within the area
of brightening are illustrated in Fig. 13. Wavefronts are indicated
rather than light rays. Unless absorption is extremely large, light
rays are normal to the wavefront. A train of plane-parallel waves is
assumed incident on the lower boundary of a refracting layer in which
the refractive-index decreases with height. When the angle of
incidence equals the critical angle, the incident waves are refracted
upon entering the refracting layer and are totally reflected at the
upper boundary The crests and troughs of the waves are indicated by
solid lines and dashed lines, respectively. At the upper boundary,
the wavefronts of the incident and reflected waves converge to a
focus. The focus is called a cusp. The upper boundary of the
refracting layer resembles a caustic,
i.e., an envelope of the moving cusps of the propagating wavefronts.
Because of the focussing of wavefronts, a large concentration of
radiant energy is usually found along the caustic (see Raman, 1959).
In the area where the incoming and outgoing wavefronts interact,
destructive interference is found along AA' and CC'
(troughs meeting crests), while constructive interference is found
along BB' (incident and reflected waves have similar phase).
Hence, brightness variations can be expected in the interference
layer, as demonstrated by Sir C. V. Raman (1959). To what extent the
microscopic effects from interference and focussing can be observed
under actual atmospheric conditions of mirage is not known.
Undoubtedly, the proper relation between refracting layer and distant
light source must be combined with an observer's position near the
upper boundary of the refracting layer. If the dark and bright bands
in the area of interference can be observed, the observer could
easily get the impression that he is viewing a rapidly oscillating
light or a light that is drawing near and moving away at rapid
intervals. Nighttime observations by airplane are most likely to
provide proper evidence of this effect.
Currently, the focussing and interference effects are the least
explored and consequently the least discussed of the various aspects
associated with optical mirage.
4. Refractive Separation of the Color Components of White Light
(Color Separation)
Due to the wavelength dependence of the optical refractive index,
systematic refraction of white light leads to a separation of the
composing colors. Visible effects of color separation are most
frequently associated with astronomical refraction. In this case,
the light enters the atmosphere at an upper boundary where n
approaches unity for all wavelengths. At an observation site near sea
level n is wavelength-dependent, so that from the upper
boundary of the atmosphere to the observation site the individual
color components are refracted at different angles. The basic
composing color of white light may be assumed to be red (24%), green
(38%), and blue-violet 38%); the red is refracted less than the
green, while the green is refracted less than the blue-violet. The
visual effects of color separation depend on the zenith
angle of the extraterrestrial light source. When a white light source
is more than 50° above the horizon, the color separation is
simply too small to be resolved by the eye. Close to the horizon it
can be observed only in the case of very small light sources. The
principle of color separation in astronomical refraction is
illustrated in Fig. 14. The light from an extended source enters the
top of the atmosphere and is separated with respect to color in the
order red, green, blue, and violet. A bundle of light rays of
diameter D can be selected for which all colors, upon
refraction, converge at O. Hence, an observer at O sees
the entire color mixture as white. When the extended source has a
diameter larger than D, an area rather than a single point of
color blending is formed. However, when the diameter of the source
becomes less than D, the point of color convergence, O,
recedes from the location of the observer. Now the observer begins to
see a gradual refractive separating of color such that red tends to
lie below green, and green tends to lie below blue-violet (see Fig.
14).
The diameter of the light beam from a given extraterrestrial source
decreases with respect to an earth-bound observer, with increasing
distance from the zenith, as illustrated in Fig. 14. Thus, when the
zenith angle increases, the apparent diameter D of the light
source decreases rapidly to a minimum value on the horizon. Hence,
the chance of having a light source of diameter less than D is
greatest on the horizon. Therefore, color separation is observed
most frequently on the horizon, when the light source is reduced to a
bright point like a star or a minute portion of the solar or lunar
disc. A prominent example of the visible effects of color
separation is the so-called Green Flash. This phenomenon is
sometimes observed when the sun disappears in a clear sky below a
distant horizon. The last star-like point can then be seen to change
rapidly from pale yellow or orange, to green, and finally, blue, or
at least a bluish-green. The vividness of the green, when the sky is
exceptionally clear, together with its almost instant appearance
and extremely short duration, has given rise to the name "green
flash" for this phenomenon.
The same gamut of colors, only in reverse order, occasionally is seen
at sunrise. The observations of the Green Flash require an unusually
clear atmosphere such that the sun is yellowish, and not red, as it
begins to sink below the horizon. A red setting sun means that the
blue and green portions of the spectrum are relatively strongly
attenuated by the atmosphere and hence indicates that conditions are
not favorable for seeing the greenish segment. Thus, the
meteorological conditions required for observing color separation are
even more stringent than those required for observing optical
mirages. Examples of color separation associated with astronomical
refraction are given on the following page in excerpts from The
Marine Observer.
In terrestrial refraction the composing colors of white light are
very seldom separated to the extent that the effects can be observed
with the naked eye. When the wavelength dependence of the refractive
index is put back into Eq. (4),
Hence, for a given temperature inversion, the refractive index
(n) decreases somewhat faster with height (z) for
Lambda = 0.4µ
(blue) than for
Lambda = 0.7µ
(red), so that the blue rays are refracted more than the red rays.
However, the difference is generally too small to be resolved by the
eye. Only under very special conditions can a visible effect be
imagined. For example, when a 100-m-thick inversion layer is assumed
to be associated with a
Delta·T = 30°C,
the change of the refractive index for blue light and red light is
respectively,
When the optical refractive indices at the lower boundary of the
inversion are
(corresponding to P =1013.3 mb and T = 15°C), values at
the upper boundary are
When white light is incident at the lower boundary of the inversion
at an angle Phio such that
then the blue rays are totally reflected by the inversion layer but
the red rays are transmitted. Hence, for
S.S. Strathnaver. Captain I. M. Sinclair. Australia to London.
Observer, Mr. J. C. Vint, Supernumerary 2nd Officer.
6th December, 1957 at 2105 S.M.T. The accompanying sketch illustrates the
changes observed in the planet as it was setting. Prismatic
binoculars were used to observe the phenomena. Position of ship:
01° 40'N.,84° 32'E.
Note. The phenomena seen at the setting of the bright planets
Venus and Jupiter Vary considerably on different occasions and are
always interesting. Sometimes no double images occur. When they are
seen, they may be of the same or different colours. The green colour is
not always seen before the instant of setting, as it was in this
observation.
(Reproduced from The Marine Observer, Vol. 28, No. 182. p. 194,
Oct. 1958)
M.V. Drina. Captain F. J. Swallow. Las Palmas to Buenos Aires.
Observer, Mr. W. M. Wheatley, Chief Officer.
28th January, 1956. At sunset the sun, when half a diameter above the
horizon, became lemon-coloured, although the shape remained normal.
The final visible segment of the sun turned to a vivid electric blue.
Visibility excellent. The sky after sunset was colourful with great
clarity of cloud shapes and colours. Cloud 3/8 Cu and Ac.
Position of ship: 18° 28's., 38° 28'w.
Note. The name of this phenomenon at sunset or sunrise is the
"green flash ", green being the colour most usually seen. It would
not be practicable to name it according to the colour observed, as
these comprise various shades of green and blue, also purple or
violet. We have had more observations of blue, purple or violet
flashes in recent years. While these colours are admittedly much less
frequently seen than various shades of green, it does appear that
they are not as rare as was form ly supposed; a probable explanation
of this is that more observers are now watching for the phenomenon.
M.V. Gloucester. Captain D. A. G. Dickens, R.N.R. Jeddah to
Suez. Observer, Mr. R. E. Baker, Chief Officer.
19th February, 1956. Abnormal refraction was observed as the sun set,
apparently shaped as shown in the sketches. The green flash was seen
all the time the upper half of the sun was disappearing,
approximately 30 sec; not only the detached pieces appeared green but
the edges of the main body as well.
Position of ship: 22° 08'N., 38° 25'E.
S.S. Pacific Northwest. Captain F. H. Perry. Panama to Los
Angeles. Observer, Mr. W. P. Crone, 4th Officer.
29th January, 1956. Half a minute before setting at bearing 262°
Venus appeared to turn bright red, becoming orange again just before
setting. At the moment of setting at 0345 G.M.T. there was an emerald
green flash of sec duration. This observation was made with the aid of
binoculars. Cloud 2/8.
Position of ship: 24° 55'N., 112° 44'W.
(Reproduced from The Marine Observer. Vol. 27. No. 175, p. 15,
Jan. 1957)
M.V. Cambridge. Captain P. P. O. Harrison. Wellington to Balboa.
Observers, the Master, Mr. P. Bower, Chief Officer, and Mr. L. Money,
4th Officer.
2nd May, 1957. When the sun rose at 0700 S.M.T. a green flash was
plainly seen. There was a bank of cumulus whose base was one sun's
diameter above the horizon and as the sun disappeared behind the
cloud a red flash occurred lasting fully 3 sec.
Position of ship: 38° 51'S 175° 1O'W.
(Reproduced from The Marine Observer, Vol. 28, No. 180, p. 77,
April 1958)
S. S. Sirsa. Captain N. Maguire. Rangoon to Cochin. Observer,
Mr. J. Richardson.
3rd December, 1950, 1755 G.M.T. Jupiter on setting showed a red spot
on the side nearest to the horizon. The spot was visible through
binoculars and telescope but not to the naked eye. The sky was clear
in the vicinity and the phenomenon was visible from the time that the
planet was 20° above the horizon.
Position of ship: 7° 40' N, 77° 47' E.
Note. When abnormal refraction is present the light of stars
or planets near the horizon tends to be elongated into a short
spectrum with the red nearest the horizon and the green and blue
farthest from the horizon. Many varieties of phenomena result,
especially in the case of the bright planets Jupiter and Venus; these
are more often seen with binoculars than with unaided vision. At
times the planet may appear double, one red and one green, or the
colour of the planet may change from red to green. In cases of
extreme refraction the planet may be seen to "swim" out with a
lateral motion, accompanied by changes of colour, usually from red to
green, with momentary returns to the normal colour of the planet. The
green flash of sunrise or sunset is an example of the same thing; the
uppermost green image of the sun limb is visible for a fraction of a
second after the sun has set.
(Reproduced from The Marine Observer, Vol. 21, No. 154, p.
214. Oct. 1951)
89° 33' 30" to 89° 33' 54", are illustrated in Fig. 15. It is
assumed that the white-light source is far away so that the incident
rays are near parallel. For Phi ~ 89° 33' 30" the blue
rays are totally reflected but the red rays penetrate the upper
boundary of the inversion. When Phio varies from
89° 33' 30" to 89° 33' 54" the red rays are alternately
transmitted and totally reflected. Hence, an observer near A may see
an elevated image that is alternately bluish and white, while an
observer at B may see a reddish image that disappears and reappears.
The small fluctuation in Phio can be produced by
atmospheric turbulence or short-period changes in the lower boundary
of the inversion. Color changes from red to green that frequently
occur when distant lights are observed can be similarly explained. In
general, visible color separation is the result of a combined action
of random and systematic atmospheric refraction.
Thus, unusual color effects that can be observed with the unaided eye
can be associated with mirage phenomena. Occurrence of these effects,
however, must be considered unusual in view of the special set of
circumstances required for their development.
5. Effects from Atmospheric Scintillation
Scintillation defines the rapid variations in apparent
brightness, position, or color of a distant luminous source when
viewed through the atmosphere. If the object lies outside the earth's
atmosphere, as in the case of stars and planets, the phenomenon is
termed astronomical scintillation; if the luminous source lies within
the atmosphere, the phenomenon is termed terrestrial scintillation.
Scintillation occurs when small-scale (meters or less)
inhomogeneities in atmospheric density interference with a
propagating wavefront for a short duration of seconds or minutes.
Such inhomogeneities are generally associated with turbulance and
convection. Turbulence and convection are most apparent in
atmospheric layers close to the earth's surface where they develop
under proper conditions of solar heating, wind velocity, and terrain.
However, they can occur also at high levels in the atmosphere.
Scintillation has been found associated with atmospheric layers near
the tropopause (30,000 to 40,000 feet).
Rapid fluctuations in brightness (scintillation in its strictest
sense) are observed most frequently. The reason for this may be that,
on the average, the time interval between moments of nearly maximum
brightness is around 1/10 of a second, a value that coincides with
the frequency to which the human eye is most sensitive. Higher
frequencies of scintillation do occur (30 to 50 per second), but
their significance is restricted to measurement made by means of
optical equipment such as telescopes. The apparent brightness
fluctuations of a distant source may be so intense that an observer
sees the light source as "flashing on and off."
Fluctuations in position are often referred to as "shimmer",
"dancing", or "wandering", and involve the apparent jerky or
continuous movement of an image about a mean point. Observations of
this phenomenon are not as common as observations of intensity
fluctuations. Under standard atmospheric conditions, position changes
vary from 1" to 30" of arc, and such displacements can hardly be
observed with the naked eye. Only under abnormal atmospheric
conditions are apparent position changes manifest. Their occurrence
is most probably in the case of point sources, i.e., sources having
no apparent diameter. Position changes of a planet like Venus or
Jupiter do occur, but actual observations are limited to very unusual
atmospheric conditions when the changes in direction of the
planet's light rays are so large as to be of the same order of
magnitude as the apparent diameter (0.5 to 1.0 minutes of arc).
In the case of an extended luminous source, a slow or rapid
"pulsation" can be observed. This contraction and expansion of the
image usually results in apparent changes of the image size.
Occasionally, pulsation of the solar or lunar limb can be observed
during setting or rising.
In general, the effects of scintillation are minimum when the
luminous source is viewed near the zenith, and maximum when the
source is viewed near the horizon. When terrestrial light sources are
involved, the scintillation increases with distance and is highly
dependent on the meteorological conditions.
The many detailed discussions of scintillation encountered in the
literature are primarily concerned with the application of optical
instruments to astronomy, optical communication, and optical
ranging.
In this case, all light sources viewed through the atmosphere exhibit
effects of scintillation irrespective of their position with respect
to the zenith. When observations are made with the unaided eye, the
above-mentioned effects of scintillation are manifested only when the
observation concern objects close to the horizon (at low elevation or
"low in the sky"). Under these conditions, the most spectacular
visual effects can be expected when the effects of scintillation
(random refraction) are superposed on any visual image that arises
from regular atmospheric refraction.
An apparent optical image formed by light scattered out of a beam by
a thin haze layer may be mistaken for a mirage. The theory of optical
propagation in a scattering, attenuating atmosphere is well covered
by Middleton (1952), an excellent reference containing much material
on vision and the visibility of objects seen through the atmosphere.
The luminance or brightness, B, in e.g. lumens/m2 , of an
extended object or optical source is invariant with distance except
for losses due to scattering or absorption along the propagation
path. Except under conditions of heavy fog, clouds, or smog,
absorption is small compared to scattering, and may be neglected. If
the scattering coefficient per unit length, O , is constant,
attenuation of a light source of intrinsic brightness B is given by
where R is the distance of range travelled by the light from the
source to the point of observation. The portion of brightness lost by
scattering out of the path is given by
this loss represents light that is scattered in all directions by the
molecules of air and aerosol particles present in the propagation
path. Secondary scattering is neglected.
The quantity Sigma·R is often called the optical depth
of an atmospheric layer, although it is a dimensionless quantity.
Thus for thin layers where Sigma·R is small, the
scattered light flux, F, in e.g. lumens, is
where F is the light flux incident on the layer.
The intensity, Is or light flux per unit solid
angle, of the light scattered from a small volume of air, v,
is the product of the incident light lfux, Fo, the
volume scattering function, Beta'(Phi), and the average
thickness of the volume. The scattering angle, Phi, is defined
in Fig. 16. The intensity of light scattered at an angle Phi
with respect to the incident beam is usually defined in terms of the
incident illuminance, E, or flux per unit area in e.g.,
lumens/m2 on an element of volume dv. This results in
hence,
which, in the case of a small scattering volume where E and
Beta'(Phi) may be considered nearly constant over the entire
volume, reduces to
The units of Beta'(Phi) are typically lumens scattered per
unit solid angle per unit volume per lumen incident light per unit
area; I(Phi) then is expressed in candles, a unit of light
intensity equal to one lumen per steradian. The volume scattering
function is normalized by
hence for an isotropic scatterer, for which
The volume scattering function relative to an isotropic scatterer is
conveniently defined as
The relative volume scattering function for very clear air has maxima
at
respectively, and a minimum of
Industrial haze, or smog, has a strong maximum at
and a minimum at
with a weaker secondary maximum at
As an example of a scattering situation, consider a very clear
atmosphere with a total vertical optical depth of 0.2; this is about
twice the optical depth of a standard atmosphere of pure air
(Middleton, (1952). The linear scattering coefficient, Phi,
for this atmosphere will be about
2x10-5 m-1 near the ground. Assume that a
haze layer one meter in thickness and with an optical depth of 0.02
exists at 100 m above
the ground; the total optical depth of the composite atmosphere will
be 0.22. The value of Sigma appropriate to the haze layer is
2x10-2 m-1,
a factor of 103 greater than for the "clear" atmosphere
above and below.
To an observer on the ground, the additional extinction of light
caused by the presence of the haze layer, amounting to only 1.6% of
the incident light from a source near the zenith, would not be
perceptible except possibly very close to the horizon. However, light
scattered out of an intense beam by the haze layer could be easily
visible. Assume that a fairly powerful light source is aimed straight
up from the ground; taking as typical values, e.g., for an automobile
sealed beam unit, an intensity, Io, of
3x104 candles (30,000 candlepower) and a beam width of
6°, the light flux Fo incident on the layer at
h = 100 m is 236 lumens, neglecting attenuation in the
air below the layer. The beam solid angle, wo, is
7.85xl0-3 steradians. The incident illuminance,
Eo, on the layer is
where the illuminated area,
A = woh2,
is 78.5m2. The scattering volume, v, is
78.5m3 since the layer is one meter thick, and the
intensity of the scattered light is
If an observer is located 100 m from the light source, he will
observe the scattered light at a distance of ~140 m and a
scattering angle, Phi, of 135°. The apparent source of the
scattered light will appear to be elliptical, roughly 4° wide and
3° high, and will present an area normal to the observer,
An, of 62.6 m2. The value of
f(Phi) for a strongly scattering medium at
Phi = 135° is about 0.2; therefore the light
Is scattered toward the observer is approximately
7.5x10-2 candles, and the apparent brightness, B,
of the scattering volume will be
A fairly dark, moonless night sky has a background brightness,
Bb of about 10-3 c/m2;
the scattered image would therefore have a total brightness of
~2.2x10-3 c/m2 and a contrast against the
night sky of
At this background brightness, data given by Middleton (1952) show
that the contrast required for 50% probability of detection for an
object of 3°-4° diameter is about 5.7x10-2; thus
the image hypothesized in this example would have a brightness about
20 times greater than the minimum detectable, and would no doubt be
easily visible as a pale, glowing, elliptical object.
In contrast, the air immediately above and below the haze layer with
Increasing the background brightness to
10-2 c/m2, corresponding to a bright,
moonlit night, would decrease the contrast of the scattered image to
1.2x10-1, which is about six times the minimum detectable
contrast at that background brightness and the image would therefore
still constitute a fairly obvious (object). Perception of light
scattered from the rest of the beam under this increased background
brightness, with
The level of background brightness for which the contrast of the
image in this example would be reduced to the point where there is
only a 50% probability of detection by an observer looking in the
right direction is roughly 10-1 c/m2; this
value corresponds to the brightness of a clear sky about 1/2 hour
after sunset.
Thus, scattering of light from sources of small beam width by
localized haze layers in the lower atmosphere may cause the
appearance of diffuse, glowing patches of light, moving with movement
of the light source, that could easily be interpreted as a UFO by an
observer unfamiliar with such phenomena. Data given by Middleton
(1952) show that with common light sources and under average
nighttime sky conditions, the main beam
of light could easily be imperceptible by scattered light, while at
the same time the light scattered from a haze patch or layer would be
easily visible to an observer; thus the source of the UFO-like image
would not be apparent.
During the last decade, active interest in optical mirage appears to
have waned. The reasons for the apparent decline are believed to be
two-fold. Firstly, on the basis of simple ray-tracing techniques,
the mirage theories satisfactorily explain the various large-scale
aspects of observations. Thus no disturbing contradictions between
theory and observation have been found. Secondly, although
atmospheric refraction remains of great interest to astronomy,
optical communication, and optical ranging, the phenomenon of the
mirage has so far failed to demonstrate a major use.
At the present time, there is no single theoretical model that
explains all the aspects, both macroscopic and microscopic, of the
mirage phenomenon. The absence of such a model must stand as evidence
that shortcomings remain in current knowledge. These shortcomings are
most eloquently discussed by Sir. C. V. Raman (1959), who suggests
and actually demonstrates that any approach to explain the phenomenon
must be based on wave-optics rather than ray-optics. The theory of
wave-optics, as applied by Sir. C. V. Raman, suggests the presence of
some intriguing aspects of the mirage that arise from the
interference and focussing of wavefronts in selected regions of the
refracting layer. Raman's experimental studies reveal that when a
collimated pencil of light is incident obliquely on a heated plate in
contact with air, the field of observation exhibits a dark region
adjacent to the plate into which the incident radiation does not
penetrate, followed by a layer in which there is an intense
concentration of light and then again by a series of dark and bright
bands of progressively diminishing intensity.
Further theoretical and experimental investigations are warranted in
order to determine to what extent the brightening and brightness
variations that arise from interference and focussing can add unusual
effects to observations of phenomenon associated with abnormal
refraction in the atmosphere.
When an unusual optical phenomenon is observed in the atmosphere, its
positive identification as a mirage cannot be made without a
physically meaningful description of what is seen and a complete set
of meteorological and astronomical data. The required "hard" data are
practically never available for the specific place and time of
observation, so that the descriptive account remains the only basis
for identification; in this case, successful identification depends
on a process of education. Thus, the casual observer of an optical
phenomenon can establish the likelihood that his observation is a
mirage only by being aware of the basic characteristics of mirage and
the physical principles that govern its appearance and behavior.
The conditions required for mirage formation and the principal
characteristics of mirage images, as described in this report, are
summarized below. The summary presents a set of standards by which to
interpret the nature of an optical observation in terms of a specific
natural atmospheric phenomenon.
Optical mirages arise from abnormal temperature gradients in the
atmosphere. A temperature decrease with height (temperature lapse)
exceeding 3.4°C per 100 m or a temperature increase with height
(temperature inversion) is most commonly responsible for a mirage
sighting.
Large temperature lapses are found in the first 10 meters above the
ground during daytime. They occur when ground surfaces are heated by
solar radiation, while during nighttime they can occur when cool air
flows over a relatively warm surface such as a lake. When the
temperature decreases with height more than 3.4° per 100 m over a
horizontal distance of 1 kilometer or more, an observer located
within the area of temperature lapse can sight an inferior mirage
near the ground (e.g., road mirage, "water" on the desert)
Layers of temperature inversion ranging in thickness from a few
meters to several hundred meters may be located on the ground or at
various levels above it. In areas where they are horizontally
extensive, an observer can sight a superior mirage that usually
appears far away (beyond 1 kilometer) and "low in the sky." The
strength of the inversion determines the degree of image-elevation;
the stronger the inversion, the higher the image appears above the
horizon. Layers of maximum temperature inversion (30°C) are
usually found adjacent to the ground.
Calm, clear-weather conditions (no precipitation or high winds) and
good horizontal visibility are favorable for mirage formation. Warm
days or warm nights during the summer are most likely to produce the
required temperature gradients.
The geometry of illumination and viewing in the case of optical
mirage is determined by the spatial variations of refraction index
that occur in the cloud-free atmosphere, and by Snell's law of
refraction, which relates these variations to changes in the
direction of propagating wavefronts. The spatial variations in
refractive index are associated with layers of temperature inversion
or temperature lapse. Variations of 3x10-5, corresponding
to temperature changes of 30°C, are considered near maximum. As a
consequence of Snell's law and the small changes in the atmospheric
refractive index, an optical mirage develops only when a temperature
inversion layer or a layer of large temperature lapse is illuminated
at grazing incidence. The requirement of grazing incidence implies
that the source of illumination must be either far away, i.e., near
the horizon, or very close to or within the layer of temperature
gradient. Therefore, both terrestrial and extraterrestrial sources
can be involved. Because of the distance factor, the actual source of
illumination may not be visible. Its location, however, must always
be in the direction in which the mirage image is observed, i.e.,
observer, image and "mirrored" source are located in the same
vertical plane.
Another consequence of Snell's law and the small spatial changes in
refractive index is that noticeable refractive effects are not likely
beyond an angular distance of approximately 14 degrees above the
horizon and that a superior mirage image is not likely beyond an
angular distance of 1 to 2 degrees above the horizon. Hence, mirages
appear "low in the sky" and near the horizontal plane of view. An
optical image seen near the zenith is not attributable to mirage.
Because of the restricted geometry between observer, mirage image,
and source of illumination, the observed image can often be made to
disappear abruptly by moving to higher or lower ground. Furthermore,
when mirage
observations are made from a continuously moving position, the image
can move also, or can move for a while and then abruptly disappear.
A mirage can involve more than one image of a single object.
Observations of up to four separate images, some inverted and some
upright, are encountered in the literature. When multiple images
occur they all lie in a single vertical plane or very close to it.
The apparent shape of a mirage can vary from clearly outlined images
of an identifiable object such as a distant ship, landscape, or the
sun or moon, to distorted images that defy any description in terms
of known objects (e.g., Fata Morgana). Apparent stretching either in
the vertical or in the horizontal plane is common.
During daytime, a mirage can appear silvery white ("water" on the
ground), or dark when projected against a bright sky background, or
it can reflect the general color of the land or seascape. Distinctly
colored images ranging from red and yellow to green and blue are
observed when unusual conditions of mirage occur near sunrise or
sunset (e.g., Red and Green Flash) or, at night, during rising or
setting of the moon or of a planet such as Venus.
In the presence of atmospheric turbulance and convection, the effects
of scintillation become superimposed on the large-scale mirage image.
When scintillation occurs, extended mirage images appear in constant
motion by changing their shape and brightness. When the image is
small and bright, as may be the case at night, large fluctuations in
brightness and under unusual conditions in color can give an illusion
of blinking, flashing, side to side oscillation, or motion toward and
away from the observer. The effects associated with scintillation can
dominate the visual appearance of any bright point-object in the area
between the horizon and approximately 14 degrees above the horizon.
The theory of ray optics adequately explains such observed
large-scale aspects of the mirage as the number of images, image
inversion, and apparent vertical stretching and shrinking. However,
if the interference and focussing of wavefronts within the refracting
layer are as fundamental
in mirage formation as purported by Sir C.V. Raman, the ray-tracing
technique may have to be replaced by the theory of wave-optics.
Sir C. V. Raman's application of wave-optics to mirage suggests that
under special conditions of illumination, the upper boundary of an
atmospheric temperature inversion could exhibit a large
concentration of radiant energy due to focussing of wavefronts. Also,
interference of wavefronts could produce alternating layers of high
and low brightness. Under what conditions and to what extent these
brightness effects can be observed in the atmosphere is not known.
Relevant observations have not been encountered in the literature,
although some unusual observations of the green flash made under
mirage conditions (O'Connel, 1958) could possibly have been caused by
the enhancement of brightness in an inversion. The visual effects
from focussing and interference of wavefronts must be considered as
the least explored aspect of mirage.
Benson, Carl S., "Ice Fog: Low Temperature Air Pollution,"
Geophysical Inst., Univ. of Alaska (November 1965).
Brocks, K., Vertikaler Temperaturgradient und terrestrische
Refraction, inshesondere ira Nochgebrge. (Verlag von Dietrich
Reimer Andrews t~ Steiner, Berlin 1939).
Dietze, Gerhard, Einfuhrung in die Optik der Atmosphare
(Akademische Verlagsgesellschaft, Geest & Portig K. - G., Leipsig
1957).
Eldridge, Ralph G., "Climatic Visibilities of the United States,"
J. Appl. Meteorol., Vol. 5, No. 3 (June 1966).
Epstein, Paul S., "Geometrical Optics in Absorbing Media," Proc.
Nat. Acad. Sci.,Vol. 16, 37-45 (1930).
Epstein, Paul S., "Reflections of Waves in an Inhomogeneous Absorbing
Medium," Proc. Nat. Acad. Sci., Vol. 16, No. 10,628-637 (October
1930).
Goos, F. and H. Haenchen, "A new and fundamental experiment on total
reflection," Ann. Physik ,Vol. 6, No. 1, pp. 333-346 (1947).
Handbook of Geophysics and Space Environments, Chapter 13, Air
Force Cambridge Research Laboratories, Office of Aerospace Research,
USAF (1965).
Hosler, Charles R., "Low-level inversion frequency in the contiguous
United States," Monthly Weather Rev., Vol. 89, No. 9 (September
1961).
Humphreys, C. E., Physics of the Air (McGraw-Hill Book Company,
Inc., New York 1940).
Jenkins, F. A., and H. E. White, Fundamentals of Optics, 3rd Ed.
(McGraw-Hill Book Company, Inc., New York 1957).
Johnson, John C., Physical Meteorology (Published jointly by the
Technology Press of M.I.T. and John Wiley & Sons, Inc., New York
1954).
Lane, J.A., "Some investigations of the structure of elevated layers
in the troposphere," J. of Atmos. and Terres. Phys., Vol. 27, pp.
969-978
Middleton, W. E. Knowles. Vision Through the Atmosphere,
University of Toronto Press, 1952.
Minnaert, M., The Nature of Light and Colour in the Open Air
(Dover Publications, Inc., 1954).
Neuberger, Hans, General Meteorological Optics, in Compendium
of Meteorology (American Meteorological Society, Boston, Mass.,
(1951).
O'Connel, D. J. K., The Green Flash and Other Low Sun Phenomena,
Vatican Observatory (North Holland Publishing Company, Amsterdam;
Interscience Publishers, Inc., New York, 1958).
Owens, James C., "Optical Refractive Index of Air: Dependence on
Pressure, Temperature and Composition," Applied Optics, Vol. 6,
No.1 (January 1967).
Pernter, J. M. and Felix M. Exner, Meteorologische Optik, (Wien
und Leipzig, Wilhelm Braumuller, K. U. K. Hofund
Universitats-Buchhandler, 1910).
Ramdas, L. A., "Micro-Climatological Investigations in India,"
Archiv. fur Meteorologie, Geophysik und Bioklimatologie, Ser. B,
Vol. 3 (1951).
Sears, F. W., Optics (Addison-Wesley Press, Inc., Cambridge,
Mass., 1949).
Tolansky, S., Optical Illusions (Pergamon Press, New York 1964).
Visher, S. S., Climatic Atlas of the United States (Harvard Univ.
Press, Cambridge, Mass. ,1954).
Wallot, S., "Der senkrechte Durchgang elektromagnetischer Wellen
durch eine Schicht raumlich veranderlicher Dielektrisitats
konstante," Ann. Physik, Vol. 60, pp. 734-762 (1919).
Wood, Robert W., Physical Optics, 3rd ed., (The MacMillan
Company, New York,1934).
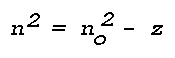
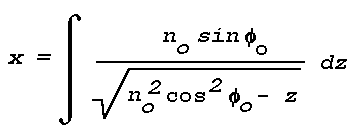
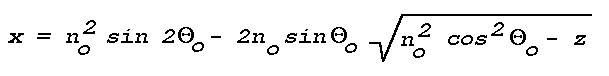
D. Partial Reflections from Atmospheric Layers
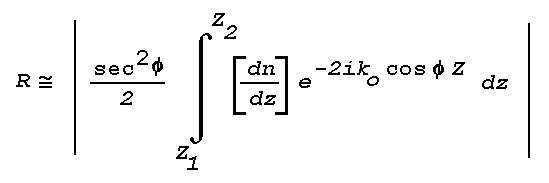
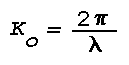
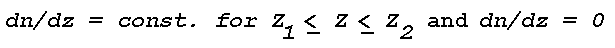
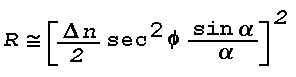
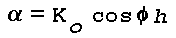
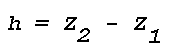
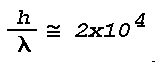
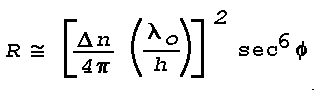
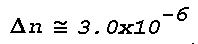
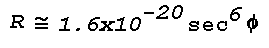
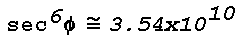
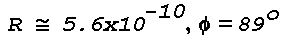
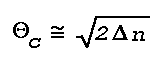
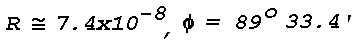
E. Spatial Variations in the Atmospheric Index-of-Refraction
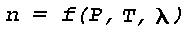
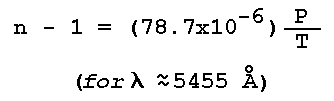
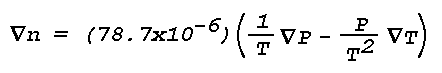
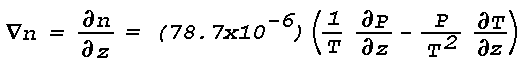
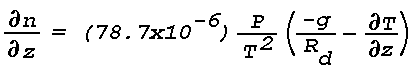
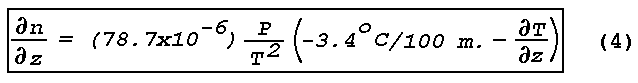
*When horizontal gradients in the refractive index are present, the
complex mirage images that occur are often referred to as Fata
Morgana. It is believed, however, that the vertical gradient is the
determining factor in the formation of most images.
Table 2
CURVATURE OF LIGHT RAYS FOR VARIOUS VALUES OF VERTICAL
TEMPERATURE GRADIENT AT STANDARD CONDITIONS OF PRESSURE
(1013.3 mb) AND TEMPERATURE (273°K)
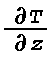
(°C/100m)
CURVATURE OF LIGHT RAYS ("/km)
-3.4
0
-1.0
5.3
-0.5
6.4
0
7.5
+6.9
22.7
+11.6
33.0
F. Meteorological Conditions Conducive to the Formation of Mirages
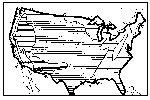
Figure 2: Normal Summer Sunshine
Click on thumbnail to see full-size image.
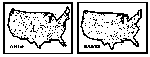
Figure 3: Inversion Frequency
Click on thumbnail to see full-size image.

Figure 4: Visibility Distribution
Click on thumbnail to see full-size image.
4. Visual Characteristics of Light-Refraction Phenomena in
the Cloud-Free Atmosphere
A. General
B. Characteristics of the Mirage
C. Light Scattering by Aerosol Particles
A. General
Figure 5: Astronomical refraction
Click on thumbnail to see full-size image.
B. Characteristics of the Mirage
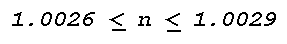
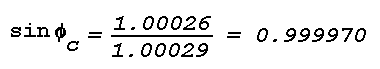
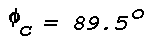
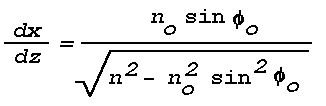
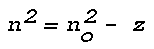
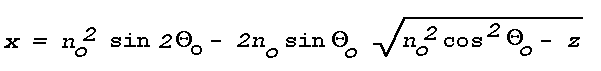
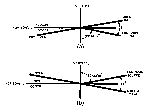
Figure 6: Mirage Geometry
Click on thumbnail to see full-size image.
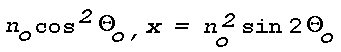
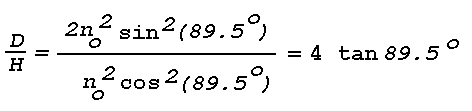

Figure 7: Light Ray Parabolas
Click on thumbnail to see full-size image.
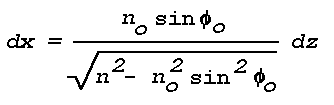
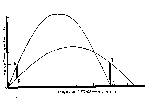
Figure 8: Image Inversion
Click on thumbnail to see full-size image.

Figure 9: Image Elongation
Click on thumbnail to see full-size image.
South Atlantic Ocean
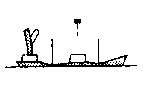
Tanker Image
Click on thumbnail to see full-size image.
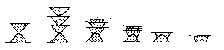
Inverted Images
Click on thumbnail to see full-size image.
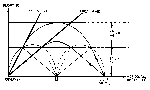
Figure 10: Double-Image Refraction
Click on thumbnail to see full-size image.
*NCAS EDITORS' NOTE: Apparent typo in the original text,
"observed" for "observer."
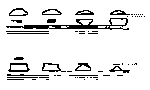
Figure 11: Sunset/Moonset Mirages
Click on thumbnail to see full-size image.
ABNORMAL REFRACTION
Off Coast of Portugal
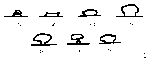
Rising Sun
Click on thumbnail to see full-size image.
ABNORMAL REFRACTION
North Atlantic Ocean
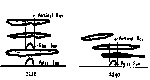
Double Sun
Click on thumbnail to see full-size image.
ABNORMAL REFRACTION
English Channel
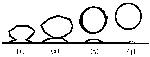
Double Sun
Click on thumbnail to see full-size image.
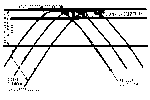
Figure 12: Energy in Inversion
Click on thumbnail to see full-size image.
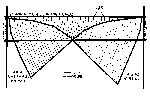
Figure 13: Wavefront Diagram
Click on thumbnail to see full-size image.
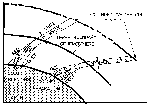
Figure 14: Refractive Color Separation
Click on thumbnail to see full-size image.
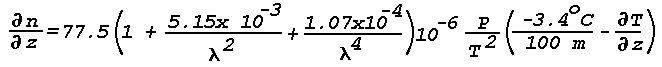
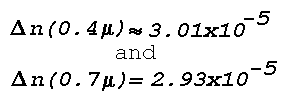
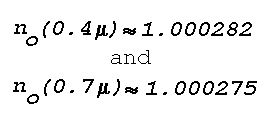
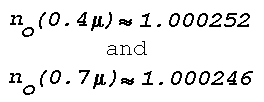

SETTING OF THE PLANET VENUS
Indian Ocean
Setting Venus
Click on thumbnail to see full-size image.
GREEN FLASH
South Atlantic Ocean
Red Sea

Green Flash
Click on thumbnail to see full-size image.
North Pacific Ocean
GREEN AND RED FLASHES
South Pacific Ocean
SETTING OF THE PLANET JUPITER
Gulf of Mannar
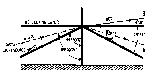
Figure 15: Refractive Color Separation Geometry
Click on thumbnail to see full-size image.
The following section on aerosol particles has been contributed
by Mr. Gordon D. Thayer of ESSA:
C. Light Scattering by Aerosol Particles
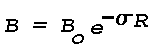
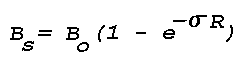
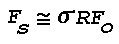
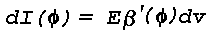
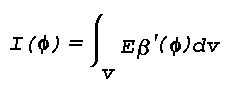
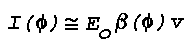

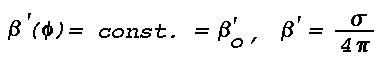
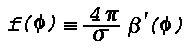
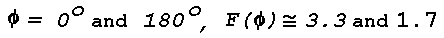
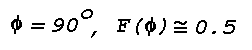
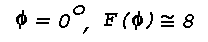
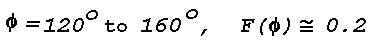
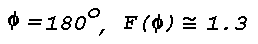
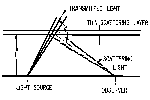
Figure 15: Light Scattering Geometry
Click on thumbnail to see full-size image.
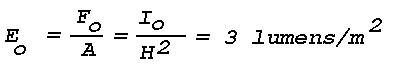
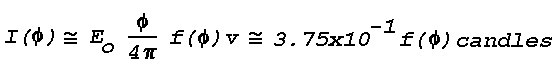
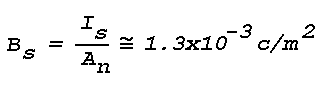
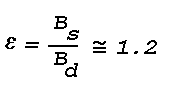
5. Evaluation of the State-of-the-Art Knowledge
6. Conclusions
A. Meteorological Conditions
B. Geometry of Illumination and Viewing
C. Shape and Color
D. Present Uncertainties
BIBLIOGRAPHY